e konstant
e konstant eller Eulers antal er en matematisk konstant. E-konstanten er reel og irrationel tal.
e = 2.718281828459 ...
Definition af e
E-konstanten er defineret som grænsen:
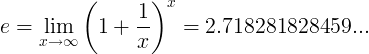
Alternative definitioner
E-konstanten er defineret som grænsen:
![]()
E-konstanten er defineret som den uendelige serie:
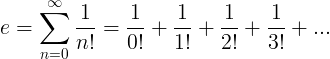
Egenskaber for e
Gensidig af e
Det gensidige af e er grænsen:
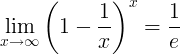
Derivater af e
Den afledte af den eksponentielle funktion er den eksponentielle funktion:
( e x ) '= e x
Den afledte af den naturlige logaritmefunktion er den gensidige funktion:
(log e x ) '= (ln x )' = 1 / x
Integraler af e
Den ubestemte integral af den eksponentielle funktion e x er den eksponentielle funktion e x .
∫ e x dx = e x + c
Den ubestemte integral af den naturlige logaritmefunktionslog e x er:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
Den bestemte integral fra 1 til e i den gensidige funktion 1 / x er 1:
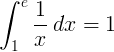
Basis e-logaritme
Den naturlige logaritme for et tal x defineres som basis e-logaritmen for x:
ln x = log e x
Eksponentiel funktion
Den eksponentielle funktion er defineret som:
f ( x ) = exp ( x ) = e x
Eulers formel
Det komplekse tal e iθ har identiteten:
e iθ = cos ( θ ) + i sin ( θ )
jeg er den imaginære enhed (kvadratroden af -1).
θ er ethvert reelt tal.
Se også
- Hvordan er 2.71828183?
- Logaritme regler
- Naturlig logaritme
- Eksponenter regler
- Normal fordeling
- Pi konstant
- e konstant - wikipedia
Advertising
TAL
- e konstant
- Eksponenter
- Fibonacci-tal
- Multiplikationstabel
- Tallsystemer
- Dele pr. Million (ppm)
- Promille (‰)
- Procent (%)
- primtal
- Nul nummer
HURTIGE TABLER