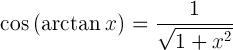Funzione arcotangente
Arctan (x), tan -1 (x), funzione tangente inversa .
Definizione di Arctan
L'arcotangente di x è definita come la funzione inversa tangente di x quando x è reale (x ∈ℝ ).
Quando la tangente di y è uguale a x:
tan y = x
Allora l'arcotangente di x è uguale alla funzione inversa tangente di x, che è uguale a y:
arctan x = tan -1 x = y
Esempio
arctan 1 = tan -1 1 = π / 4 rad = 45 °
Grafico di arctan
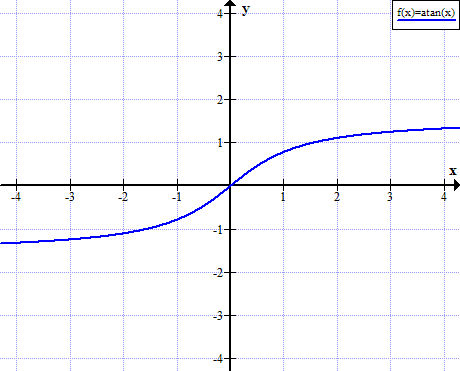
Arctan governa
| Nome regola | Regola |
|---|---|
| Tangente dell'arcotangente |
tan (arctan x ) = x |
| Arctan di argomenti negativi |
arctan (- x ) = - arctan x |
| Somma Arctan |
arctan α + arctan β = arctan [( α + β ) / (1- αβ )] |
| Differenza di Arctan |
arctan α - arctan β = arctan [( α - β ) / (1+ αβ )] |
| Seno di arcotangente |
|
| Coseno di arcotangente |
|
| Argomento reciproco |
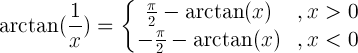 |
| Arctan da arcsin |
|
| Derivato di arctan |
|
| Integrale indefinito di arctan |
|
Tavolo Arctan
| x | arctan (x) (rad) |
arctan (x) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1.2490 | -71,565 ° |
| -2 | -1.1071 | -63,435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0,5 | -0.4636 | -26,565 ° |
| 0 | 0 | 0 ° |
| 0,5 | 0.4636 | 26,565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63,435 ° |
| 3 | 1.2490 | 71,565 ° |
| ∞ | π / 2 | 90 ° |
Guarda anche
- Funzione tangente
- Funzione arcoseno
- Funzione arcoseno
- Arctan di 0
- Arctan di 1
- Arctan di 2
- Arctan dell'infinito
- Derivato di arctan
- Integrale di arctan
- Seno di arctan
- Coseno di arctan
- Grafico di Arctan
- Calcolatrice Arctan
- Convertitore da gradi a radianti
Advertising
TRIGONOMETRIA
TAVOLI RAPIDI