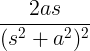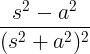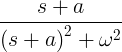首页/数学/微积分/拉普拉斯变换

拉普拉斯变换

拉普拉斯变换功能
拉普拉斯变换表
拉普拉斯变换属性
拉普拉斯变换的例子

拉普拉斯变换通过从零到无穷大的积分将时域函数转换为s域函数

时域函数的乘以e ^-st。

拉普拉斯（Laplace）变换用于快速找到微分方程和积分的解。

时域中的导数在s域中转换为乘以s。

时域中的积分转换为s域中的s除。

拉普拉斯变换功能

拉普拉斯变换是使用L {}运算符定义的：

$F（s）= \数学{L} \左\ {f（t）\右\} = \ int_ {0} ^ {\ infty} e ^ {-st} f（t）dt$

拉普拉斯逆变换

拉普拉斯逆变换可以直接计算。

通常，逆变换是从变换表中给出的。

拉普拉斯变换表

功能名称	时域功能	拉普拉斯变换
功能名称	f（t）	F（s）= L { f（t）}
不变	1	$\ frac {1} {s}$
线性的	t	$\ frac {1} {s ^ 2}$
功率	Ť ^ñ	$\ frac {n！} {s ^ {n + 1}}$
功率	Ť^一	Γ（一个+1）⋅小号^{- （一+1）}
指数	Ë^在	$\ frac {1} {sa}$
正弦波	罪于	$\ frac {a} {s ^ 2 + a ^ 2}$
余弦	cos at	$\ frac {s} {s ^ 2 + a ^ 2}$
双曲正弦	SINH在	$\ frac {a} {s ^ 2-a ^ 2}$
双曲余弦	COSH在	$\ frac {s} {s ^ 2-a ^ 2}$
正弦波	Ť罪在	$\ frac {2as} {（s ^ 2 + a ^ 2）^ 2}$
余弦增长	t cos在	$\ frac {s ^ 2-a ^ 2} {（s ^ 2 + a ^ 2）^ 2}$
正弦衰减	Ë ^-at罪ωT	$\ frac {\ omega} {\ left（s + a \ right）^ 2 + \ omega ^ 2}$
衰减余弦	Ë ^-at COS ωT	$\ frac {s + a} {\ left（s + a \ right）^ 2 + \ omega ^ 2}$
三角函数	δ（吨）	1
延迟三角洲	δ（ta）	Ë ^-as

拉普拉斯变换属性

物业名称	时域功能	拉普拉斯变换	评论
	f（t）	F（s）
线性度	af（t）+ bg（t）	aF（s）+ bG（s）	a，b是常数
规模变化	f（at）	$\ frac {1} {a} F \ left（\ frac {s} {a} \ right）$	一/ 0
转移	e ^-at f（t）	F（s + a）
延迟	f（ta）	ë ^-如˚F（小号）
推导	$\ frac {df（t）} {dt}$	sF（s）-f（0）
第N次推导	$\ frac {d ^ nf（t）} {dt ^ n}$	s ⁿ f（s）-s ^{n -1}f（0）-s ^{n -2}f '（0）-...- f ^{（n -1）}（0）
功率	t ⁿ f（t）	$（-1）^ n \ frac {d ^ nF（s）} {ds ^ n}$
积分	$\ int_ {0} ^ {t} f（x）dx$	$\ frac {1} {s} F（s）$
倒数	$\ frac {1} {t} f（t）$	$\ int_ {s} ^ {\ infty} F（x）dx$
卷积	f（t）* g（t）	˚F（小号）⋅ ģ（小号）	*是卷积运算符
周期性功能	f（t）= f（t + T）	$\ frac {1} {1-e ^ {-sT}} \ int_ {0} ^ {T} e ^ {-sx} f（x）dx$

拉普拉斯变换的例子

例子1

求f（t）的变换：

f（t）= 3 t + 2 t ²

解：

ℒ{ t } = 1 / s ²

ℒ{ t ² } = 2 / s ³

F（s）=ℒ{ f（t）} =ℒ{3 t + 2 t ² } =3ℒ{ t } +2ℒ{ t ² } = 3 / s ² + 4 / s ³

范例＃2

求F（s）的逆变换：

F（s）= 3 /（s ² + s -6）

解：

为了找到逆变换，我们需要将s域函数更改为更简单的形式：

F（s）= 3 /（s ² + s -6）= 3 / [（s -2）（s +3）] = a /（s -2）+ b /（s +3）

[ a（s +3）+ b（s -2）] / [（s -2）（s +3）] = 3 / [（s -2）（s +3）]

a（s +3）+ b（s -2）= 3

为了找到a和b，我们得到2个方程-s系数之一，其余的第二个：

（a + b）s + 3 a -2 b = 3

a + b = 0，3 a -2 b = 3

a = 3/5，b = -3/5

F（s）= 3/5（s -2）-3/5 （s +3）

现在，可以通过使用指数函数的转换表轻松转换F（s）：

f（t）=（3/5）e ^{2 t-}（3/5）e ^{-3 t}

也可以看看

💬

结石

快速表格