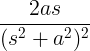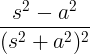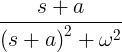تحويل لابلاس
تحويل لابلاس يحول دالة المجال الزمني إلى دالة المجال s بالتكامل من الصفر إلى اللانهاية
لدالة المجال الزمني ، مضروبة في e -st .
يتم استخدام تحويل لابلاس لإيجاد حلول للمعادلات التفاضلية والتكاملات بسرعة.
يتحول الاشتقاق في المجال الزمني إلى الضرب بـ s في المجال s.
يتم تحويل التكامل في المجال الزمني إلى القسمة على s في المجال s.
وظيفة تحويل لابلاس
يتم تعريف تحويل لابلاس بالمعامل L {}:
![]()
معكوس تحويل لابلاس
يمكن حساب تحويل لابلاس المعكوس مباشرة.
عادة ما يتم إعطاء التحويل العكسي من جدول التحويلات.
طاولة تحويل لابلاس
| اسم وظيفة | وظيفة المجال الزمني | تحويل لابلاس |
|---|---|---|
و ( ر ) |
F ( s ) = L { f ( t )} |
|
| ثابت | 1 | |
| خطي | ر | |
| قوة | ر ن |
|
| قوة | ر أ |
Γ ( أ +1) ⋅ ث - ( أ +1) |
| الأس | البريد في |
|
| شرط | الخطيئة في |
|
| جيب التمام | كوس في |
|
| الجيب الزائدي |
سينه في |
|
| جيب التمام الزائدي |
كوش في |
|
| تزايد الجيب |
ر الخطيئة في |
|
| تزايد جيب التمام |
t cos في |
|
| الجيب المتحلل |
ه -على الخطيئة ωt |
|
| جيب التمام المتحلل |
ه -على كوس ωt |
|
| دالة دلتا |
δ ( ر ) |
1 |
| دلتا متأخرة |
δ ( تا ) |
ه- as |
خصائص تحويل لابلاس
| اسم الخاصية | وظيفة المجال الزمني | تحويل لابلاس | تعليق |
|---|---|---|---|
و ( ر ) |
و ( ق ) |
||
| الخطية | af ( t ) + bg ( t ) | aF ( ق ) + bG ( ق ) | أ ، ب ثابتة |
| تغيير الحجم | و ( في ) |
|
أ / 0 |
| تحول | e -at f ( t ) | F ( s + a ) | |
| تأخير | و ( تا ) | ه - مثل F ( ق ) | |
| الاشتقاق |
|
sF ( s ) - و (0) | |
| الاشتقاق من العشر |
|
ث ن و ( ث ) - ث ن -1 و (0) - ث ن -2 و '(0) -...- و ( ن -1) (0) | |
| قوة | ر ن و ( ر ) |
|
|
| دمج |
|
|
|
| متبادل |
|
|
|
| التفاف | و ( ر ) * ز ( ر ) | و ( ق ) ⋅ G ( ق ) | * هو عامل الالتفاف |
| الوظيفة الدورية | و ( ر ) = و ( تي + تي ) |
|
أمثلة تحويل لابلاس
مثال 1
أوجد تحويل f (t):
و ( ر ) = 3 ر + 2 ر 2
المحلول:
ℒ { t } = 1 / ثانية 2
ℒ { t 2 } = 2 / ثانية 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
المثال رقم 2
أوجد التحويل العكسي لـ F (s):
F ( ق ) = 3 / ( ث 2 + ث - 6)
المحلول:
لإيجاد التحويل العكسي ، نحتاج إلى تغيير دالة المجال s إلى صيغة أبسط:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
أ ( ق +3) + ب ( ق -2) = 3
لإيجاد a و b ، نحصل على معادلتين - أحد معاملي s والثاني من الباقي:
( أ + ب ) ث + 3 أ -2 ب = 3
أ + ب = 0 ، 3 أ -2 ب = 3
أ = 3/5 ، ب = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
يمكن الآن تحويل F (s) بسهولة باستخدام جدول التحويلات لوظيفة الأس:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
أنظر أيضا
Advertising
حساب التفاضل والتكامل
- حد
- المشتق
- متكامل
- سلسلة
- تحويل لابلاس
- التفاف
- رموز التفاضل والتكامل
جداول سريعة