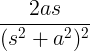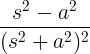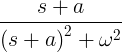Transformada de Laplace

La transformada de Laplace converteix una funció de domini temporal en funció de domini s mitjançant la integració de zero a infinit

 de la funció de domini temporal, multiplicat per e -st .

La transformada de Laplace s’utilitza per trobar ràpidament solucions per a equacions diferencials i integrals.

La derivació en el domini temporal es transforma en multiplicació per s en el domini s.

La integració en el domini temporal es transforma en divisió per s en el domini s.

Funció de transformada de Laplace

La transformada de Laplace es defineix amb l' operador L {}:

F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt

Transformada de Laplace inversa

La transformada inversa de Laplace es pot calcular directament.

Normalment, la transformada inversa es dóna a partir de la taula de transformades.

Taula de transformada de Laplace

Nom de la funció Funció de domini temporal Transformada de Laplace

f ( t )

F ( s ) = L { f ( t )}
Constant 1 \ frac {1} {s}
Lineal t \ frac {1} {s ^ 2}
Potència

t n

\ frac {n!} {s ^ {n + 1}}
Potència

t a

Γ ( a +1) ⋅ s - ( a +1)
Exponent

e at

\ frac {1} {sa}
Sinus

pecar a

\ frac {a} {s ^ 2 + a ^ 2}
Cosinus

cos at

\ frac {s} {s ^ 2 + a ^ 2}
Sinus hiperbòlic

sinh at

\ frac {a} {s ^ 2-a ^ 2}
Cosinus hiperbòlic

cosh at

\ frac {s} {s ^ 2-a ^ 2}
Sinus creixent

t sin at

\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}
Cosinus en creixement

t cos at

\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}
Sinus en descomposició

e -at sin ωt

\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}
Cosinus en descomposició

e -at cos ωt

\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}
Funció Delta

δ ( t )

1

Delta retardat

δ ( ta )

e -as

Propietats de la transformada de Laplace

Nom de la propietat Funció de domini temporal Transformada de Laplace Comenta
 

f ( t )

V ( s )

  
Linealitat af ( t ) + bg ( t ) aF ( s ) + bG ( s ) a , b són constants
Canvi d’escala f ( a ) \ frac {1} {a} F \ left (\ frac {s} {a} \ right) a / 0
Maj e -at f ( t ) F ( s + a )  
Retard f ( ta ) e - com F ( s )  
Derivació \ frac {df (t)} {dt} sF ( s ) - f (0)  
N-e derivació \ frac {d ^ nf (t)} {dt ^ n} s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0)  
Potència t n f ( t ) (-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}  
Integració \ int_ {0} ^ {t} f (x) dx \ frac {1} {s} F (s)  
Recíproc \ frac {1} {t} f (t) \ int_ {s} ^ {\ infty} F (x) dx  
Convolució f ( t ) * g ( t ) F ( s ) ⋅ G ( s ) * és l'operador de convolució
Funció periòdica f ( t ) = f ( t + T ) \ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx  

Exemples de transformada de Laplace

Exemple 1

Trobeu la transformada de f (t):

f ( t ) = 3 t + 2 t 2

Solució:

ℒ { t } = 1 / s 2

ℒ { t 2 } = 2 / s 3

F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3

 

Exemple 2

Trobeu la transformada inversa de F (s):

F ( s ) = 3 / ( s 2 + s - 6)

Solució:

Per trobar la transformada inversa, hem de canviar la funció de domini s a una forma més senzilla:

F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

Per trobar a i b, obtenim 2 equacions: un dels coeficients s i la segona de la resta:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, b = -3/5

F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)

Ara F (s) es poden transformar fàcilment utilitzant la taula de transformacions per a la funció exponent:

f ( t ) = (3/5) e 2 t - (3/5) e -3 t

 

Vegeu també

Advertising

CÀLCUL
TAULES RÀPIDES