Funkce Arcsine
arcsin (x), sin -1 (x), inverzní sinusová funkce.
Definice Arcsin
Arcsine x je definována jako inverzní sinusová funkce x, když -1≤x≤1.
Když se sinus y rovná x:
sin y = x
Pak se arcsine x rovná inverzní sinusové funkci x, která se rovná y:
arcsin x = sin -1 x = y
Příklad
arcsin 1 = hřích -1 1 = π / 2 rad = 90 °
Graf arcsinu
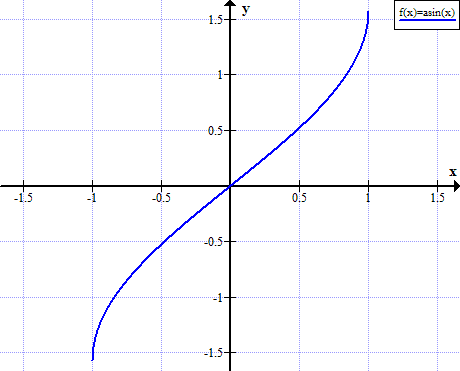
Arcsinova pravidla
| Název pravidla | Pravidlo |
|---|---|
| Sinus arcsinu | sin (arcsin x ) = x |
| Arcsine ze sinu | arcsin (sin x ) = x +2 k π, když k ∈ℤ ( k je celé číslo) |
| Arcsin negativního argumentu | arcsin (- x ) = - arcsin x |
| Doplňkové úhly | arcsin x = π / 2 - arccos x = 90 ° - arccos x |
| Součet arcsinů | arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Arcsinův rozdíl | arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Kosinus arcsinu | |
| Tečna arkusinu | |
| Derivát arcsinu | 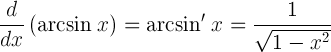 |
| Neurčitý integrál arcsinu |
Arcsinův stůl
| x | arcsin (x) (rad) |
arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Viz také
- Sinusová funkce
- Funkce arkkosinu
- Funkce Arctan
- Arcsin kalkulačka
- Převodník stupňů na radiány
- Arcsin od 0
- Arcsin z 1
- Arcsin nekonečna
- Arcsinův graf
- Derivát arcsinu
- Arcsinův integrál
- Hřích arcsinu
- Protože arcsin
- Tan arcsin
Advertising