Konvolution

Konvolution er korrelationsfunktionen for f (τ) med den omvendte funktion g (t-τ).

Konvolutionsoperatøren er stjernesymbolet * .

Faldet af f (t) og g (t) er lig med integralet af f (τ) gange f (t-τ):

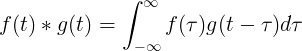
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Konvolution af 2 diskrete funktioner er defineret som:

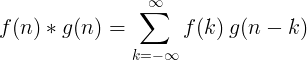
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2-dimensionel diskret foldning bruges normalt til billedbehandling.

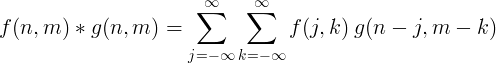
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

Vi kan filtrere det diskrete indgangssignal x (n) ved foldning med impulssvaret h (n) for at få udgangssignalet y (n).

y ( n ) = x ( n ) * h ( n )

Fouriertransformationen af en multiplikation af 2 funktioner er lig med foldningen af Fouriertransformationerne for hver funktion:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Fouriertransformationen af en opløsning af 2 funktioner er lig med multiplikationen af Fouriertransformationerne for hver funktion:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Se også