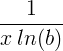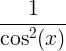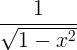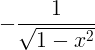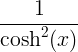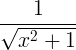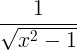Παράγοντες κανόνες

Παράγωγοι κανόνες και νόμοι. Πίνακας παραγώγων συναρτήσεων.

• Παράγωγος ορισμός
• Παράγοντες κανόνες
• Πίνακας παραγώγων συναρτήσεων
• Παράγωγα παραδείγματα

Παράγωγος ορισμός

Το παράγωγο μιας συνάρτησης είναι ο λόγος της διαφοράς της τιμής συνάρτησης f (x) στα σημεία x + Δx και x με Δx, όταν το Δx είναι άπειρα μικρό. Το παράγωγο είναι η κλίση συνάρτησης ή η κλίση της εφαπτομένης γραμμής στο σημείο x.

Δεύτερο παράγωγο

Το δεύτερο παράγωγο δίνεται από:

Ή απλώς αντλήστε το πρώτο παράγωγο:

Nth παράγωγο

Το n th παράγωγο υπολογίζεται με απορρέουν f (x) n φορές.

Τα n th παράγωγο είναι ίσο με το παράγωγο του (n-1) παράγωγο:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] "

Παράδειγμα:

Βρείτε το τέταρτο παράγωγο του

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] "" = [10 x ⁴ ] "" = [40 x ³ ] "= [120 x ² ]" = 240 x

Παράγωγο στο γράφημα της συνάρτησης

Το παράγωγο μιας συνάρτησης είναι η κλίση της εφαπτομενικής γραμμής.

Παράγοντες κανόνες

Παράγωγος κανόνας αθροίσματος	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Κανόνας παραγώγων προϊόντων	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Παράγωγος κανόνας πηλίκου
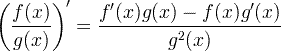Παράγωγος κανόνας αλυσίδας	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Παράγωγος κανόνας αθροίσματος

Όταν τα a και b είναι σταθερές.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Παράδειγμα:

Βρείτε το παράγωγο του:

3 x ² + 4 x.

Σύμφωνα με τον κανόνα αθροίσματος:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Κανόνας παραγώγων προϊόντων

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Παράγωγος κανόνας πηλίκου

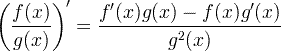
Παράγωγος κανόνας αλυσίδας

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Αυτός ο κανόνας μπορεί να γίνει καλύτερα κατανοητός με τη σημείωση του Lagrange:

Λειτουργική γραμμική προσέγγιση

Για μικρά Δx, μπορούμε να πάρουμε μια προσέγγιση στο f (x ₀ + Δx), όταν γνωρίζουμε f (x ₀ ) και f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Πίνακας παραγώγων συναρτήσεων

Όνομα συνάρτησης	Λειτουργία	Παράγωγο
	στ ( x )	f '( x )
Συνεχής	υπ	0
Γραμμικός	x	1
Εξουσία	x α	ax α- 1
Εκθετικός	ε x	ε x
Εκθετικός	ένα x	a x ln α
Φυσικός λογάριθμος	ln ( x )
Λογάριθμος	log b ( x )
Ημίτονο	αμαρτία x	cos x
Συνημίτονο	cos x	-σεχ x
Εφαπτομένος	μαύρισμα x
Αρκσίνη	τόξο x
Αρκοσίνη	arccos x
Arctangent	Αρκταν x
Υπερβολικό ημίτονο	Σινχ x	κοχ x
Υπερβολικό συνημίτονο	κοχ x	Σινχ x
Υπερβολική εφαπτομένη	tanh x
Αντίστροφο υπερβολικό ημίτονο	sinh -1 x
Αντίστροφο υπερβολικό συνημίτονο	cosh -1 x
Αντίστροφη υπερβολική εφαπτομένη	tanh -1 x

Παράγωγα παραδείγματα

Παράδειγμα # 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Παράδειγμα # 2

f ( x ) = αμαρτία (3 x ² )

Κατά την εφαρμογή του κανόνα αλυσίδας:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Δεύτερο παράγωγο τεστ

Όταν το πρώτο παράγωγο μιας συνάρτησης είναι μηδέν στο σημείο x ₀ .

f '( x ₀ ) = 0

Στη συνέχεια, το δεύτερο παράγωγο στο σημείο x ₀ , f "(x ₀ ), μπορεί να υποδείξει τον τύπο αυτού του σημείου:

Δείτε επίσης

• Λογισμός
• Μετασχηματισμός Laplace ( ℒ  )
• Λογιστικά σύμβολα