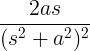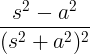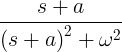Μετασχηματισμός Laplace

Ο μετασχηματισμός Laplace μετατρέπει μια συνάρτηση τομέα χρόνου σε συνάρτηση s-domain με ενσωμάτωση από μηδέν σε άπειρο

της συνάρτησης τομέα χρόνου, πολλαπλασιαζόμενη με το e ^-st .

Ο μετασχηματισμός Laplace χρησιμοποιείται για γρήγορη εύρεση λύσεων για διαφορικές εξισώσεις και ολοκληρώματα.

Το παράγωγο στον τομέα χρόνου μετατρέπεται σε πολλαπλασιασμό κατά s στον τομέα s.

Η ενσωμάτωση στον τομέα χρόνου μετατρέπεται σε διαίρεση κατά s στον τομέα s.

Λειτουργία μετασχηματισμού Laplace

Ο μετασχηματισμός Laplace ορίζεται με τον τελεστή L {}:

$F (s) = \ mathcal {L} \ αριστερά \ {f (t) \ δεξιά \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Ο αντίστροφος μετασχηματισμός Laplace μπορεί να υπολογιστεί απευθείας.

Συνήθως ο αντίστροφος μετασχηματισμός δίνεται από τον πίνακα μετασχηματισμών.

Όνομα συνάρτησης	Συνάρτηση τομέα χρόνου	Μετασχηματισμός Laplace
Όνομα συνάρτησης	στ ( τ )	F ( s ) = L { f ( t )}
Συνεχής	1	$\ frac {1} {s}$
Γραμμικός	τ	$\ frac {1} {s ^ 2}$
Εξουσία	t ^ν	$\ frac {n!} {s ^ {n + 1}}$
Εξουσία	τ ^α	Γ ( a +1) ⋅ s ^{- ( a +1)}
Εκθέτης	ε ^σε	$\ frac {1} {sa}$
Ημίτονο	αμαρτία στο	$\ frac {a} {s ^ 2 + a ^ 2}$
Συνημίτονο	cos στο	$\ frac {s} {s ^ 2 + a ^ 2}$
Υπερβολικό ημίτονο	Σινχ στο	$\ frac {a} {s ^ 2-a ^ 2}$
Υπερβολικό συνημίτονο	κοίτα στο	$\ frac {s} {s ^ 2-a ^ 2}$
Καλλιέργεια ημιτονοειδούς	t αμαρτία σε	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Αυξανόμενο συνημίτονο	t cos σε	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Ημιτονοειδές	e ^-at sin ωt	$\ frac {\ omega} {\ αριστερά (s + a \ δεξιά) ^ 2 + \ ωμέγα ^ 2}$
Παρακμή συνημίτονο	e ^-at cos ωt	$\ frac {s + a} {\ αριστερά (s + a \ δεξιά) ^ 2 + \ ωμέγα ^ 2}$
Συνάρτηση Delta	δ ( τ )	1
Καθυστέρηση δέλτα	δ ( ta )	ε- ^ως

Ονομα ιδιοκτησίας	Συνάρτηση τομέα χρόνου	Μετασχηματισμός Laplace	Σχόλιο
	στ ( τ )	F ( ες )
Γραμμικότητα	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b είναι σταθερά
Αλλαγή κλίμακας	στ ( στο )	$\ frac {1} {a} F \ αριστερά (\ frac {s} {a} \ δεξιά)$	α / 0
Μετατόπιση	e ^-at f ( τ )	F ( s + α )
Καθυστέρηση	f ( ta )	ε ^{- ως} F ( ες )
Παραγωγή	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
Β-παράγωγο	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Εξουσία	t ⁿ στ ( τ )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Ενσωμάτωση	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (ες)$
Αμοιβαίος	$\ frac {1} {t} στ (τ)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Περιελιγμός	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* είναι ο χειριστής της συνέλιξης
Περιοδική συνάρτηση	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$