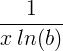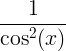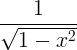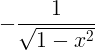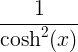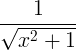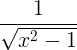व्युत्पन्न नियम

व्युत्पन्न नियम और कानून। कार्यों की तालिका तालिका।

व्युत्पन्न परिभाषा

किसी फ़ंक्शन की व्युत्पत्ति, बिंदु x + Δx और x के साथ x पर फ़ंक्शन मान f (x) के अंतर का अनुपात है, जब isx असीम रूप से छोटा होता है। व्युत्पन्न फ़ंक्शन एक्स या बिंदु x पर स्पर्शरेखा रेखा का ढलान है।

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

दूसरा व्युत्पन्न

दूसरा व्युत्पन्न निम्न द्वारा दिया गया है:

या बस पहला व्युत्पन्न प्राप्त करें:

च '' (x) = (च '(x))'

नौवां व्युत्पन्न

N वें व्युत्पन्न f (x) एन बार पाने की जाती है।

N वें व्युत्पन्न है की (n-1) व्युत्पन्न व्युत्पन्न के बराबर:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

उदाहरण:

के चौथे व्युत्पन्न का पता लगाएं

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '' = [40 x 3 ] '' = [120 x 2 ] '= 240 x

फ़ंक्शन के ग्राफ पर व्युत्पन्न

एक फ़ंक्शन का व्युत्पन्न स्पर्शरेखा रेखा का ढलान है।

व्युत्पन्न नियम

व्युत्पन्न राशि नियम

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
व्युत्पन्न उत्पाद नियम

( f ( x ) ( g ( x )) '= f' ( x ) g ( x ) + f ( x ) जी ' ( x )
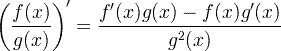व्युत्पन्न भागफल नियम \ बाएँ (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( एक्स)}
व्युत्पन्न श्रृंखला नियम

f ( g ( x )) '= f' ( g ( x )) ( g ' ( x )

व्युत्पन्न राशि नियम

जब ए और बी लगातार होते हैं।

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

उदाहरण:

इसका व्युत्पन्न खोजें:

3 x 2 + 4 x।

राशि नियम के अनुसार:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3 x2 x + 4 =1 = 6 x + 4

व्युत्पन्न उत्पाद नियम

( f ( x ) ( g ( x )) '= f' ( x ) g ( x ) + f ( x ) जी ' ( x )

व्युत्पन्न भागफल नियम

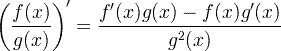
\ बाएँ (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( एक्स)}

व्युत्पन्न श्रृंखला नियम

f ( g ( x )) '= f' ( g ( x )) ( g ' ( x )

इस नियम को लाग्रेंज के अंकन से बेहतर समझा जा सकता है:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

फंक्शन रैखिक सन्निकटन

छोटे fx के लिए, हम f (x 0 + ) x ) के लिए एक अनुमान लगा सकते हैं , जब हम f (x 0 ) और f '(x 0 ) जानते हैं :

f ( x 0 + Δ x ) x f ( x 0 ) + f '( x 0 ) Δ x

कार्यों की तालिका तालिका

कार्य का नाम समारोह यौगिक

च ( x )

 f '( x )
लगातार

स्थिरांक

0

रैखिक

x

1

शक्ति

x a

कुल्हाड़ी a- १
घातीय

ई एक्स

ई एक्स
घातीय

a x

a x ln a
प्राकृतिक

ln ( x )

लोगारित्म

लॉग बी ( एक्स )

ज्या

पाप x

cos x
कोसाइन

cos x

-सीन एक्स
स्पर्शरेखा

तन x

arcsine

आर्क्सिन एक्स

कोटिकोज्या

arccos x

arctangent

अर्कटन x
हाइपरबोलिक साइन

पाप x

cosh x
हाइपरबोलिक कॉशन

cosh x

पाप x
अतिशयोक्तिपूर्ण स्पर्शज्या

तन्ह x

हाइपरबोलिक साइन उलटा

पाप -1 एक्स

व्युत्क्रम हाइपरबोलिक कोसाइन

cosh -1 एक्स

उलटा स्पर्शवर्धक स्पर्शज्या

तनह -1 x

व्युत्पन्न उदाहरण

उदाहरण 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2 ( 5 x + 1 + 0 = 3 x 2 +10 x +1

उदाहरण # 2

f ( x ) = sin (3 x 2 )

चेन नियम लागू करते समय:

f ' ( x ) = cos (3 x 2 ) x [3 x 2 ]' = cos (3 x 2 ) = -6 x

दूसरा व्युत्पन्न परीक्षण

जब किसी फ़ंक्शन का पहला व्युत्पन्न बिंदु x 0 पर शून्य होता है ।

f '( x 0 ) = 0

तब बिंदु x 0 , f '' (x 0 ) पर दूसरा व्युत्पन्न, उस बिंदु के प्रकार को इंगित कर सकता है:

 

f '' ( x 0 )/ 0

 स्थानीय न्यूनतम

f '' ( x 0 ) <0

 स्थानीय अधिकतम

f '' ( x 0 ) = 0

 अनपेक्षित

 

यह सभी देखें

Advertising

कैलकुलस
रैपिड टाइलें