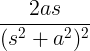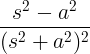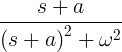Trasformata di Laplace

La trasformata di Laplace converte una funzione nel dominio del tempo in una funzione nel dominio s mediante integrazione da zero a infinito

 della funzione nel dominio del tempo, moltiplicata per e -st .

La trasformata di Laplace viene utilizzata per trovare rapidamente soluzioni per equazioni differenziali e integrali.

La derivazione nel dominio del tempo viene trasformata in moltiplicazione per s nel dominio s.

L'integrazione nel dominio del tempo viene trasformata in divisione per s nel dominio s.

Funzione trasformata di Laplace

La trasformata di Laplace è definita con l' operatore L {}:

F (s) = \ mathcal {L} \ sinistra \ {f (t) \ destra \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt

Trasformata di Laplace inversa

La trasformata inversa di Laplace può essere calcolata direttamente.

Di solito la trasformata inversa è data dalla tabella delle trasformazioni.

Tabella di trasformazione di Laplace

Nome della funzione Funzione nel dominio del tempo Trasformata di Laplace

f ( t )

F ( s ) = L { f ( t )}
Costante 1 \ frac {1} {s}
Lineare t \ frac {1} {s ^ 2}
Energia

t n

\ frac {n!} {s ^ {n + 1}}
Energia

t a

Γ ( a +1) ⋅ s - ( a +1)
Esponente

e a

\ frac {1} {sa}
Sine

peccato a

\ frac {a} {s ^ 2 + a ^ 2}
Coseno

cos a

\ frac {s} {s ^ 2 + a ^ 2}
Seno iperbolico

sinh at

\ frac {a} {s ^ 2-a ^ 2}
Coseno iperbolico

cosh a

\ frac {s} {s ^ 2-a ^ 2}
Seno crescente

t peccato a

\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}
Coseno in crescita

t cos a

\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}
Seno in decomposizione

e -at sin ωt

\ frac {\ omega} {\ sinistra (s + a \ destra) ^ 2 + \ omega ^ 2}
Coseno in decomposizione

e -at cos ωt

\ frac {s + a} {\ sinistra (s + a \ destra) ^ 2 + \ omega ^ 2}
Funzione delta

δ ( t )

1

Delta ritardato

δ ( ta )

e -as

Proprietà della trasformata di Laplace

Nome della proprietà Funzione nel dominio del tempo Trasformata di Laplace Commento
 

f ( t )

F ( s )

  
Linearità af ( t ) + bg ( t ) aF ( s ) + bG ( s ) a , b sono costanti
Cambio di scala f ( a ) \ frac {1} {a} F \ sinistra (\ frac {s} {a} \ destra) a / 0
Cambio e -at f ( t ) F ( s + a )  
Ritardo f ( ta ) e - come F ( s )  
Derivazione \ frac {df (t)} {dt} sF ( s ) - f (0)  
Derivazione ennesima \ frac {d ^ nf (t)} {dt ^ n} s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0)  
Energia t n f ( t ) (-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}  
Integrazione \ int_ {0} ^ {t} f (x) dx \ frac {1} {s} F (s)  
Reciproco \ frac {1} {t} f (t) \ int_ {s} ^ {\ infty} F (x) dx  
Convoluzione f ( t ) * g ( t ) F ( s ) ⋅ G ( s ) * è l'operatore di convoluzione
Funzione periodica f ( t ) = f ( t + T ) \ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx  

Esempi di trasformata di Laplace

Esempio 1

Trova la trasformata di f (t):

f ( t ) = 3 t + 2 t 2

Soluzione:

ℒ { t } = 1 / s 2

ℒ { t 2 } = 2 / s 3

F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3

 

Esempio n. 2

Trova la trasformata inversa di F (s):

F ( s ) = 3 / ( s 2 + s - 6)

Soluzione:

Per trovare la trasformata inversa, dobbiamo cambiare la funzione di dominio s in una forma più semplice:

F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

Per trovare aeb, otteniamo 2 equazioni: uno dei coefficienti s e il secondo del resto:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, b = -3/5

F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)

Ora F (s) può essere trasformato facilmente utilizzando la tabella delle trasformazioni per la funzione esponente:

f ( t ) = (3/5) e 2 t - (3/5) e -3 t

 

Guarda anche

Advertising

CALCOLO
TAVOLI RAPIDI