ಫೈಬೊನಾಕಿ ಸಂಖ್ಯೆಗಳು ಮತ್ತು ಅನುಕ್ರಮ

ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮವು ಸಂಖ್ಯೆಗಳ ಅನುಕ್ರಮವಾಗಿದೆ, ಅಲ್ಲಿ ಪ್ರತಿ ಸಂಖ್ಯೆಯು 0 ಮತ್ತು 1 ರ ಮೊದಲ ಎರಡು ಸಂಖ್ಯೆಗಳನ್ನು ಹೊರತುಪಡಿಸಿ 2 ಹಿಂದಿನ 2 ಸಂಖ್ಯೆಗಳ ಮೊತ್ತವಾಗಿರುತ್ತದೆ.

• ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮ ಸೂತ್ರ
• ಸುವರ್ಣ ಅನುಪಾತ ಒಮ್ಮುಖ
• ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮ ಕೋಷ್ಟಕ
• ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮ ಕ್ಯಾಲ್ಕುಲೇಟರ್
• ಫೈಬೊನಾಕಿ ಕ್ರಿಯೆಯ ಸಿ ++ ಕೋಡ್

ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮ ಸೂತ್ರ

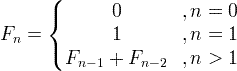
ಉದಾಹರಣೆಗೆ:

ಎಫ್ ₀ = 0

ಎಫ್ ₁ = 1

ಎಫ್ ₂ = ಎಫ್ ₁ + ಎಫ್ ₀ = 1 + 0 = 1

ಎಫ್ ₃ = ಎಫ್ ₂ + ಎಫ್ ₁ = 1 + 1 = 2

ಎಫ್ ₄ = ಎಫ್ ₃ + ಎಫ್ ₂ = 2 + 1 = 3

ಎಫ್ ₅ = ಎಫ್ ₄ + ಎಫ್ ₃ = 3 + 2 = 5

...

ಸುವರ್ಣ ಅನುಪಾತ ಒಮ್ಮುಖ

ಎರಡು ಅನುಕ್ರಮ ಫಿಬೊನಾಕಿ ಸಂಖ್ಯೆಗಳ ಅನುಪಾತವು ಸುವರ್ಣ ಅನುಪಾತಕ್ಕೆ ಒಮ್ಮುಖವಾಗುತ್ತದೆ:

φ ಎಂಬುದು ಸುವರ್ಣ ಅನುಪಾತ = (1 + √ 5 ) / 2 ≈ 1.61803399

ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮ ಕೋಷ್ಟಕ

n	ಎಫ್ ಎನ್
0	0
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233
14	377
15	610
16	987
17	1597
18	2584
19	4181
20	6765

ಫೈಬೊನಾಕಿ ಅನುಕ್ರಮ ಕ್ಯಾಲ್ಕುಲೇಟರ್

ಟಿಬಿಡಿ

ಫೈಬೊನಾಕಿ ಕ್ರಿಯೆಯ ಸಿ ಕೋಡ್

double Fibonacci(unsigned int n)

{

    double f_n =n;

    double f_n1=0.0;

    double f_n2=1.0;

 

    if( n / 1 ) {

        for(int k=2; k<=n; k++) {

            f_n  = f_n1 + f_n2;

            f_n2 = f_n1;

            f_n1 = f_n;

        }

    }

 

    return f_n;

}