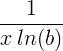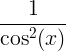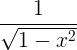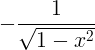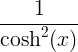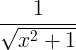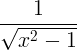Išvestinės taisyklės

Išvestinės taisyklės ir įstatymai. Funkcijų lentelės išvestinės.

Išvestinė apibrėžtis
Išvestinės taisyklės
Funkcijų lentelės išvestinės
Išvestiniai pavyzdžiai

Išvestinė apibrėžtis

Funkcijos išvestinė yra funkcijos f (x) taškų x + Δx ir x ir Δx taškų skirtumo santykis, kai Δx yra be galo mažas. Išvestinė yra liestinės tiesės funkcijos nuolydis arba nuolydis taške x.

$f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}$

Antrasis vedinys

Antrasis išvestinis yra pateiktas:

Arba tiesiog išveskite pirmąjį darinį:

N-tasis vedinys

N -oji darinys yra apskaičiuojamas išvedant f (x) n kartų.

Kad n -ojo išvestinės yra lygi darinys, kurio (n-1) darinys:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Pavyzdys:

Raskite ketvirtąjį darinį iš

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] "" "= [10 x ⁴ ]" "= [40 x ³ ]" = [120 x ² ] "= 240 x

Išvestinė funkcijos grafike

Funkcijos išvestinė yra tangentinės tiesės nuolydis.

Išvestinės taisyklės

Išvestinės sumos taisyklė	( af ( x ) + bg ( x )) = = af ( x ) + bg ' ( x )
Išvestinių produktų taisyklė	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
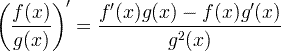Išvestinė koeficiento taisyklė	$\ kairė (\ frac {f (x)} {g (x)} \ dešinė) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}$
Išvestinė grandinės taisyklė	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Išvestinės sumos taisyklė

Kai a ir b yra konstantos.

( af ( x ) + bg ( x )) = = af ( x ) + bg ' ( x )

Pavyzdys:

Raskite darinį iš:

3 x ² + 4 x.

Pagal sumos taisyklę:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Išvestinių produktų taisyklė

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Išvestinė koeficiento taisyklė

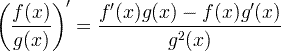
$\ kairė (\ frac {f (x)} {g (x)} \ dešinė) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}$

Išvestinė grandinės taisyklė

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Šią taisyklę galima geriau suprasti naudojant Lagrange'o užrašą:

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

Funkcijos linijinis aproksimavimas

Mažam Δx galime gauti apytikslę reikšmę f (x ₀ + Δx), kai žinome f (x ₀ ) ir f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Funkcijų lentelės išvestinės

Funkcijos pavadinimas	Funkcija	Išvestinė
Funkcijos pavadinimas	f ( x )	f '( x )
Nuolatinis	konst	0
Linijinis	x	1
Galia	x ^a	kirvis ^a-¹
Eksponentinis	e ^x	e ^x
Eksponentinis	a ^x	a ^x ln a
Natūralus logaritmas	ln ( x )
Logaritmas	log _b ( x )
Sinusas	nuodėmė x	cos x
Kosinusas	cos x	-sin x
Tangentas	įdegis x
Arcsine	„arcsin x“
Arkosinas	arccos x
Arkangangentas	„arktanas x“
Hiperbolinis sinusas	sinh x	cosh x
Hiperbolinis kosinusas	cosh x	sinh x
Hiperbolinis liestinis	tanh x
Atvirkštinis hiperbolinis sinusas	sinh ^-1 x
Atvirkštinis hiperbolinis kosinusas	cosh ^-1 x
Atvirkštinė hiperbolinė liestinė	tanh ^-1 x