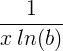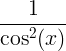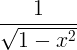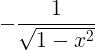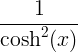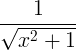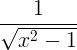Atvasinātie noteikumi
Atvasinātie noteikumi un likumi. Funkciju atvasinājumi tabula.
Atvasinājuma definīcija
Funkcijas atvasinājums ir funkcijas f (x) starpības attiecība punktos x + Δx un x ar Δx, kad Δx ir bezgalīgi mazs. Atvasinājums ir pieskares līnijas funkcijas slīpums vai slīpums punktā x.
![]()
Otrais atvasinājums
Otro atvasinājumu dod:
![]()
Vai vienkārši atvasiniet pirmo atvasinājumu:
![]()
N atvasinājums
N th atvasinājums tiek aprēķināta pēc iespējas labāk f (x) n reizes.
The n th atvasinājumu ir vienāda ar atvasinājums no (n-1) atvasinājums:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Piemērs:
Atrodiet ceturto atvasinājumu no
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' = [40 x 3 ] '' = [120 x 2 ] '= 240 x
Atvasinājums uz funkcijas grafika
Funkcijas atvasinājums ir tangenciālās līnijas slīpums.
Atvasinātie noteikumi
| Atvasinātās summas noteikums |
( af ( x ) + bg ( x )) "= af" ( x ) + bg " ( x ) |
| Atvasināta produkta noteikums |
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Atvasinātā koeficienta noteikums |
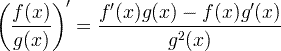 |
| Atvasināto ķēžu likums |
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Atvasinātās summas noteikums
Kad a un b ir konstantes.
( af ( x ) + bg ( x )) "= af" ( x ) + bg " ( x )
Piemērs:
Atrodiet atvasinājumu no:
3 x 2 + 4 x.
Saskaņā ar summas likumu:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Atvasināta produkta noteikums
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Atvasinātā koeficienta noteikums
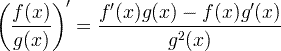
Atvasināto ķēžu likums
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Šo noteikumu labāk var saprast ar Lagranža apzīmējumu:
![]()
Funkciju lineārā aproksimācija
Mazam Δx mēs varam iegūt tuvinājumu f (x 0 + Δx), kad mēs zinām f (x 0 ) un f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Funkciju atvasinājumi tabula
| Funkcijas nosaukums | Funkcija | Atvasinājums |
|---|---|---|
|
f ( x ) |
f '( x ) | |
| Pastāvīgs |
konst |
0 |
| Lineāra |
x |
1 |
| Jauda |
x a |
cirvis a- 1 |
| Eksponenciāls |
e x |
e x |
| Eksponenciāls |
a x |
a x ln a |
| Dabiskais logaritms |
ln ( x ) |
|
| Logaritms |
log b ( x ) |
|
| Sine |
grēks x |
cos x |
| Kosinuss |
cos x |
-sin x |
| Tangents |
iedegums x |
|
| Arcsine |
arcsin x |
|
| Arkosīns |
arccos x |
|
| Arktangents |
arctan x |
|
| Hiperboliska sinusa |
sinh x |
cosh x |
| Hiperboliskais kosinuss |
cosh x |
sinh x |
| Hiperboliska pieskare |
tanh x |
|
| Apgrieztā hiperboliskā sinusa |
sinh -1 x |
|
| Apgrieztais hiperboliskais kosinuss |
cosh -1 x |
|
| Apgrieztais hiperboliskais tangenss |
tanh -1 x |
|
Atvasinājumu piemēri
1. piemērs
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
2. piemērs
f ( x ) = grēks (3 x 2 )
Piemērojot ķēdes kārtulu:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Otrais atvasinājumu tests
Kad funkcijas pirmais atvasinājums ir nulle punktā x 0 .
f '( x 0 ) = 0
Tad otrais atvasinājums punktā x 0 , f '' (x 0 ), var norādīt šī punkta tipu:
|
f '' ( x 0 )/ 0 |
vietējais minimums |
|
f '' ( x 0 ) <0 |
vietējais maksimums |
|
f '' ( x 0 ) = 0 |
nenoteikts |
Skatīt arī
Advertising
KALKULS
- Ierobežot
- Atvasinājums
- Neatņemama
- Sērija
- Laplasa transformācija
- Konversija
- Rēķina simboli
ĀTRAS TABULAS