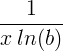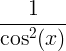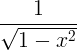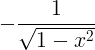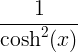ഡെറിവേറ്റീവ് നിയമങ്ങൾ

ഡെറിവേറ്റീവ് നിയമങ്ങളും നിയമങ്ങളും. ഫംഗ്ഷനുകൾ പട്ടികയുടെ ഡെറിവേറ്റീവുകൾ.

ഡെറിവേറ്റീവ് നിർവചനം

ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ് x + Δx പോയിന്റുകളിലെ x (x), x withx എന്ന പോയിന്റിലെ ഫംഗ്ഷൻ മൂല്യത്തിന്റെ വ്യത്യാസത്തിന്റെ അനുപാതമാണ്, x അനന്തമായി ചെറുതായിരിക്കുമ്പോൾ. പോയിന്റ് x ലെ ടാൻജെന്റ് ലൈനിന്റെ ഫംഗ്ഷൻ ചരിവ് അല്ലെങ്കിൽ ചരിവാണ് ഡെറിവേറ്റീവ്.

 

f '(x) = \ lim _ {\ ഡെൽറ്റ x \ മുതൽ 0} \ frac {f (x + \ ഡെൽറ്റ x) -f (x)} {\ ഡെൽറ്റ x}

രണ്ടാമത്തെ ഡെറിവേറ്റീവ്

രണ്ടാമത്തെ ഡെറിവേറ്റീവ് നൽകുന്നത്:

അല്ലെങ്കിൽ ആദ്യത്തെ ഡെറിവേറ്റീവ് നേടുക:

f '' (x) = (f '(x))'

Nth ഡെറിവേറ്റീവ്

N ാം ഡെറിവേറ്റീവ് F (X) N തവണ നിർണയിക്കാനുള്ള കണക്കാക്കുന്നത്.

N ാം ഡെറിവേറ്റീവ് ആയ (N-1) വ്യതിരിക്ത ഡെറിവേറ്റീവായ തുല്യമാണ്:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

ഉദാഹരണം:

ന്റെ നാലാമത്തെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '[[40 x 3 ]' '= [120 x 2 ]' = 240 x

ഫംഗ്ഷന്റെ ഗ്രാഫിൽ ഡെറിവേറ്റീവ്

ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ് ടാൻജൻഷ്യൽ ലൈനിന്റെ ചരിവാണ്.

ഡെറിവേറ്റീവ് നിയമങ്ങൾ

ഡെറിവേറ്റീവ് സം റൂൾ

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
ഡെറിവേറ്റീവ് ഉൽപ്പന്ന നിയമം

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
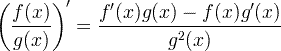ഡെറിവേറ്റീവ് ഘടക റൂൾ \ ഇടത് (\ frac {f (x)} {g (x)} \ വലത്) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
ഡെറിവേറ്റീവ് ചെയിൻ റൂൾ

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

ഡെറിവേറ്റീവ് സം റൂൾ

എപ്പോൾ ഒരു ആൻഡ് ബി സ്ഥിരാങ്കങ്ങളും ആകുന്നു.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

ഉദാഹരണം:

ഇതിന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക:

3 x 2 + 4 x.

തുക നിയമം അനുസരിച്ച്:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

ഡെറിവേറ്റീവ് ഉൽപ്പന്ന നിയമം

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

ഡെറിവേറ്റീവ് ഘടക റൂൾ

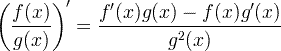
\ ഇടത് (\ frac {f (x)} {g (x)} \ വലത്) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

ഡെറിവേറ്റീവ് ചെയിൻ റൂൾ

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

ലഗ്രാഞ്ചിന്റെ നൊട്ടേഷൻ ഉപയോഗിച്ച് ഈ നിയമം നന്നായി മനസ്സിലാക്കാൻ കഴിയും:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} x dx}

ഫംഗ്ഷൻ ലീനിയർ ഏകദേശീകരണം

ചെറിയ Δx ന്, f (x 0 +), f (x 0 ), f '(x 0 ) എന്നിവ അറിയുമ്പോൾ നമുക്ക് f (x 0 + Δx) ലേക്ക് ഒരു ഏകദേശ രൂപം ലഭിക്കും :

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) x

ഫംഗ്ഷനുകൾ പട്ടികയുടെ ഡെറിവേറ്റീവുകൾ

പ്രവർത്തനത്തിന്റെ പേര് പ്രവർത്തനം ഡെറിവേറ്റീവ്

f ( x )

 f '( x )
നിരന്തരമായ

const

0

ലീനിയർ

x

1

പവർ

x a

കോടാലി a- 1
എക്‌സ്‌പോണൻഷ്യൽ

e x

e x
എക്‌സ്‌പോണൻഷ്യൽ

ഒരു x

a x ln a
സ്വാഭാവിക ലോഗരിതം

ln ( x )

ലോഗരിതം

ലോഗ് ബി ( x )

സൈൻ

പാപം x

cos x
കോസിൻ

cos x

-സിൻ x
ടാൻജെന്റ്

ടാൻ x

ആർക്ക്സൈൻ

arcsin x

ആർക്കോസിൻ

ആർക്കോസ് x

ആർക്റ്റാൻജന്റ്

ആർക്ടാൻ x
ഹൈപ്പർബോളിക് സൈൻ

sinh x

cosh x
ഹൈപ്പർബോളിക് കോസൈൻ

cosh x

sinh x
ഹൈപ്പർബോളിക് ടാൻജെന്റ്

tanh x

വിപരീത ഹൈപ്പർബോളിക് സൈൻ

sinh -1 x

വിപരീത ഹൈപ്പർബോളിക് കോസൈൻ

cosh -1 x

വിപരീത ഹൈപ്പർബോളിക് ടാൻജെന്റ്

tanh -1 x

ഡെറിവേറ്റീവ് ഉദാഹരണങ്ങൾ

ഉദാഹരണം # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

ഉദാഹരണം # 2

f ( x ) = പാപം (3 x 2 )

ചെയിൻ റൂൾ പ്രയോഗിക്കുമ്പോൾ:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

രണ്ടാമത്തെ ഡെറിവേറ്റീവ് ടെസ്റ്റ്

ഒരു ഫംഗ്ഷന്റെ ആദ്യ ഡെറിവേറ്റീവ് x 0 പോയിന്റിൽ പൂജ്യമാകുമ്പോൾ .

f '( x 0 ) = 0

X 0 , f '' (x 0 ) ലെ രണ്ടാമത്തെ ഡെറിവേറ്റീവിന് ആ പോയിന്റിന്റെ തരം സൂചിപ്പിക്കാൻ കഴിയും:

 

f '' ( x 0 )/ 0

 പ്രാദേശിക മിനിമം

f '' ( x 0 ) <0

 പ്രാദേശിക പരമാവധി

f '' ( x 0 ) = 0

 നിർണ്ണയിക്കപ്പെട്ടിട്ടില്ല

 

ഇതും കാണുക

Advertising

കാൽക്കുലസ്
ദ്രുത പട്ടികകൾ