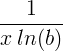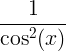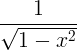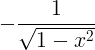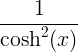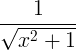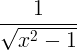Afgeleide regels

Afgeleide regels en wetten. Afgeleide functietabel.

• Afgeleide definitie
• Afgeleide regels
• Afgeleide functietabel
• Afgeleide voorbeelden

Afgeleide definitie

De afgeleide van een functie is de verhouding van het verschil van functiewaarde f (x) op punten x + Δx en x met Δx, wanneer Δx oneindig klein is. De afgeleide is de functiehelling of helling van de raaklijn op punt x.

 

Tweede afgeleide

De tweede afgeleide wordt gegeven door:

Of leid eenvoudig de eerste afgeleide af:

N-de afgeleide

De n- th derivaat wordt berekend door het afleiden f (x) n maal.

De n de afgeleide is gelijk aan de afgeleide van de (n-1) afgeleide:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Voorbeeld:

Zoek de vierde afgeleide van

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]' = 240 x

Afgeleide op grafiek van functie

De afgeleide van een functie is de helling van de tangentiële lijn.

Afgeleide regels

Afgeleide som regel	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Afgeleide productregel	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Afgeleide quotiëntregel
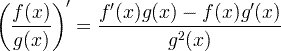Afgeleide kettingregel	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Afgeleide som regel

Als a en b constanten zijn.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Voorbeeld:

Zoek de afgeleide van:

3 x ² + 4 x.

Volgens de somregel:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Afgeleide productregel

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Afgeleide quotiëntregel

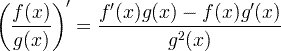
Afgeleide kettingregel

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Deze regel kan beter worden begrepen met de notatie van Lagrange:

Functie lineaire benadering

Voor kleine Δx kunnen we een benadering krijgen van f (x ₀ + Δx), als we f (x ₀ ) en f '(x ₀ ) kennen:

f ( x ₀ + Δ X ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Afgeleide functietabel

Functienaam	Functie	Derivaat
	f ( x )	f '( x )
Constante	const	0
Lineair	x	1
Kracht	x een	bijl a- 1
Exponentieel	e x	e x
Exponentieel	een x	een x ln een
Natuurlijke logaritme	ln ( x )
Logaritme	log b ( x )
Sinus	zonde x	cos x
Cosinus	cos x	-sin x
Raaklijn	bruin x
Arcsine	arcsin x
Arccosine	arccos x
Arctangens	arctan x
Hyperbolische sinus	sinh x	cosh x
Hyperbolische cosinus	cosh x	sinh x
Hyperbolische tangens	tanh x
Inverse hyperbolische sinus	sinh -1 x
Inverse hyperbolische cosinus	cosh -1 x
Inverse hyperbolische tangens	tanh -1 x

Afgeleide voorbeelden

Voorbeeld 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Voorbeeld 2

f ( x ) = zonde (3 x ² )

Bij het toepassen van de kettingregel:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Tweede afgeleide test

Wanneer de eerste afgeleide van een functie nul is op punt x ₀ .

f '( x ₀ ) = 0

Dan kan de tweede afgeleide op punt x ₀ , f '' (x ₀ ), het type van dat punt aangeven:

 

f '' ( x 0 )/ 0	lokaal minimum
f '' ( x 0 ) <0	lokaal maximum
f '' ( x 0 ) = 0	onbepaald

 

---

Zie ook

• Calculus
• Laplace-transformatie ( ℒ  )
• Calculus symbolen