Distribuția probabilității

În probabilitate și statistici, distribuția este o caracteristică a unei variabile aleatoare, descrie probabilitatea variabilei aleatoare în fiecare valoare.

Fiecare distribuție are o anumită funcție de densitate a probabilității și funcție de distribuție a probabilității.

Deși există un număr nedefinit de distribuții de probabilitate, există mai multe distribuții comune în uz.

Funcția de distribuție cumulativă

Distribuția probabilității este descrisă de funcția de distribuție cumulativă F (x),

care este probabilitatea ca variabila aleatorie X să obțină o valoare mai mică sau egală cu x:

F ( x ) = P ( X ≤ x )

Distribuție continuă

Funcția de distribuție cumulativă F (x) este calculată prin integrarea funcției densității probabilității f (u) a variabilei aleatoare continue X.

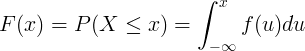
Distribuție discretă

Funcția de distribuție cumulativă F (x) se calculează prin însumarea funcției de probabilitate a masei P (u) a variabilei discrete aleatorii X.

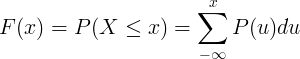
Tabel de distribuții continue

Distribuția continuă este distribuția unei variabile aleatoare continue.

Exemplu de distribuție continuă

...

Tabel de distribuții continue

Numele distribuției Simbol de distribuție Funcția densității probabilității (pdf) Rău Varianța
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussian

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniformă

X ~ U ( a , b )

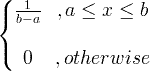 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, altfel \ end {matrix} \ frac {(ba) ^ 2} {12}
Exponențială X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
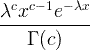Gamma X ~ gamma ( c , λ) \ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi pătrat

X ~ χ 2 ( k )

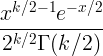 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log-normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Taxă        
Orez        
Studentul este t        

Tabel de distribuții discrete

Distribuția discretă este distribuția unei variabile aleatorii discrete.

Exemplu de distribuție discretă

...

Tabel de distribuții discrete

Numele distribuției Simbol de distribuție Funcția de masă a probabilității (pmf) Rău Varianța
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binom

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniformă

X ~ U ( a, b )

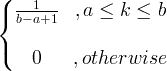 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, altfel \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geometric

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hiper-geometrică

X ~ HG ( N , K , n )

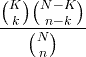N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Berna ( p )

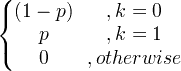 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, altfel \ end {matrix}

p

p (1- p )

 

Vezi si

Advertising

PROBABILITATE ȘI STATISTICĂ
MESE RAPIDE