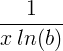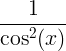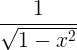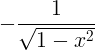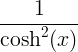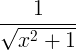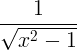Izvedena pravila

Izvedena pravila in zakoni. Tabela derivatov funkcij.

• Izvedena definicija
• Izvedena pravila
• Tabela derivatov funkcij
• Izvedeni primeri

Izvedena definicija

Izpeljanka funkcije je razmerje razlike vrednosti funkcije f (x) v točkah x + Δx in x z Δx, kadar je Δx neskončno majhna. Izpeljanka je naklon funkcije ali naklon tangente v točki x.

 

Druga izpeljanka

Drugi izpeljan je podan z:

Ali preprosto izpeljati prvi izpeljanko:

N-ti odvod

N th derivat se meri z izpeljavo f (x) n-krat.

V n th derivat, ki je enak derivat s (n-1) derivata:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Primer:

Poiščite četrto izpeljanko iz

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] "" "= [10 x ⁴ ]" "= [40 x ³ ]" = = 120 x ² ] '= 240 x

Izpeljanka na grafu funkcije

Izpeljanka funkcije je naklon tangencialne črte.

Izvedena pravila

Pravilo izpeljane vsote	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Pravilo o izvedenih izdelkih	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Izpeljano pravilo količnika
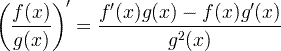Pravilo izpeljane verige	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Pravilo izpeljane vsote

Ko sta a in b konstanti.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Primer:

Poiščite izpeljanko iz:

3 x ² + 4 x.

V skladu s pravilom vsote:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Pravilo o izvedenih izdelkih

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Izpeljano pravilo količnika

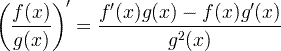
Pravilo izpeljane verige

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

To pravilo lahko bolje razumemo z Lagrangeovim zapisom:

Funkcionalni linearni približek

Za majhne Δx lahko dobimo približek f (x ₀ + Δx), če poznamo f (x ₀ ) in f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Tabela derivatov funkcij

Ime funkcije	Funkcija	Izvedeni finančni instrumenti
	f ( x )	f '( x )
Stalno	const	0
Linearno	x	1
Moč	x a	sekira a- 1
Eksponentno	e x	e x
Eksponentno	a x	a x ln a
Naravni logaritem	ln ( x )
Logaritem	dnevnik b ( x )
Sinus	greh x	cos x
Cosine	cos x	-greh x
Tangenta	porjavelost x
Arcsine	arcsin x
Arccosine	arccos x
Arktangens	arctan x
Hiperbolični sinus	sinh x	cosh x
Hiperbolični kosinus	cosh x	sinh x
Hiperbolični tangens	tanh x
Inverzni hiperbolični sinus	sinh -1 x
Inverzni hiperbolični kosinus	cosh -1 x
Inverzni hiperbolični tangens	tanh -1 x

Izvedeni primeri

Primer # 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

2. primer

f ( x ) = greh (3 x ² )

Pri uporabi pravila verige:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Drugi test izpeljank

Ko je prvi odvod funkcije nič v točki x ₀ .

f '( x ₀ ) = 0

Potem lahko drugi odvod v točki x ₀ , f "(x ₀ ), označuje vrsto te točke:

 

f '' ( x 0 )/ 0	lokalni minimum
f '' ( x 0 ) <0	lokalni maksimum
f "( x 0 ) = 0	nedoločeno

 

---

Poglej tudi

• Račun
• Laplasova transformacija ( ℒ  )
• Simboli računa