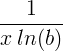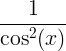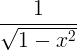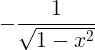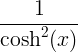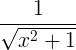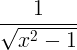Derivatregler

Derivatregler och lagar. Derivat av funktionstabellen.

• Derivatdefinition
• Derivatregler
• Derivat av funktionstabellen
• Derivata exempel

Derivatdefinition

Derivat av en funktion är förhållandet mellan skillnaden i funktionsvärde f (x) vid punkterna x + Δx och x med Δx, när Δx är oändligt liten. Derivatet är funktionslutningen eller lutningen för tangentlinjen vid punkt x.

 

Andra derivat

Det andra derivatet ges av:

Eller härled helt enkelt det första derivatet:

N: t derivat

Det n: e derivatet beräknas genom att härleda f (x) n gånger.

Det n: e derivatet är lika med derivatet av (n-1) derivatet:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Exempel:

Hitta det fjärde derivatet av

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' [10 x ⁴ ] '' = [40 x ³ ] '' = [120 x ² ] '= 240 x

Derivat på diagram över funktion

Derivat av en funktion är den tangentiella linjens lutning.

Derivatregler

Derivat summan regel	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Derivatproduktregel	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Derivatkvotientregel
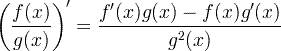Derivat kedjeregel	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Derivat summan regel

När a och b är konstanter.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Exempel:

Hitta derivatet av:

3 x ² + 4 x.

Enligt summaregeln:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Derivatproduktregel

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Derivatkvotientregel

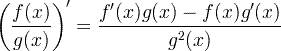
Derivat kedjeregel

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Denna regel kan förstås bättre med Lagranges notation:

Funktion linjär approximation

För små Δx kan vi få en approximation till f (x ₀ + Δx), när vi vet f (x ₀ ) och f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Derivat av funktionstabellen

Funktionsnamn	Fungera	Derivat
	f ( x )	f '( x )
Konstant	konst	0
Linjär	x	1
Kraft	x a	yxa a- 1
Exponentiell	e x	e x
Exponentiell	a x	a x ln a
Naturlig logaritm	ln ( x )
Logaritm	log b ( x )
Sinus	sin x	cos x
Cosinus	cos x	-sin x
Tangent	solbränna x
Arcsine	bågsin x
Arccosine	arccos x
Arktangent	arctan x
Hyperbolisk sinus	sinh x	cosh x
Hyperbolisk cosinus	cosh x	sinh x
Hyperbolisk tangent	tanh x
Invers hyperbolisk sinus	sinh -1 x
Invers hyperbolisk cosinus	cosh -1 x
Invers hyperbolisk tangent	tanh -1 x

Derivata exempel

Exempel 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Exempel 2

f ( x ) = sin (3 x ² )

När du använder kedjeregeln:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Andra derivat test

När det första derivatet av en funktion är noll vid punkten x ₀ .

f '( x ₀ ) = 0

Då kan det andra derivatet vid punkt x ₀ , f '' (x ₀ ), ange typen av den punkten:

 

f '' ( x 0 )/ 0	lokalt minimum
f '' ( x 0 ) <0	lokal max
f '' ( x 0 ) = 0	obestämd

 

---

Se även

• Kalkyl
• Laplace-transform ( ℒ  )
• Kalkylsymboler