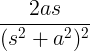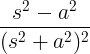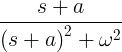Laplace Transform

Laplace-transform omvandlar en tidsdomänfunktion till s-domänfunktion genom integration från noll till oändlighet

av tidsdomänfunktionen multiplicerad med e ^-st .

Laplace-transformen används för att snabbt hitta lösningar för differentialekvationer och integraler.

Derivation i tidsdomänen transformeras till multiplikation med s i s-domänen.

Integration i tidsdomänen omvandlas till division av s i s-domänen.

Laplace-transformfunktion

Laplace-transformen definieras med L {} -operatören:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Den omvända Laplace-transformationen kan beräknas direkt.

Vanligtvis ges den inversa transformen från transformationstabellen.

Funktionsnamn	Tidsdomänfunktion	Laplace-omvandling
Funktionsnamn	f ( t )	F ( s ) = L { f ( t )}
Konstant	1	$\ frac {1} {s}$
Linjär	t	$\ frac {1} {s ^ 2}$
Kraft	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Kraft	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Exponent	e ^vid	$\ frac {1} {sa}$
Sinus	synda vid	$\ frac {a} {s ^ 2 + a ^ 2}$
Cosinus	cos vid	$\ frac {s} {s ^ 2 + a ^ 2}$
Hyperbolisk sinus	sinh på	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolisk cosinus	kosa på	$\ frac {s} {s ^ 2-a ^ 2}$
Växande sinus	t syndar vid	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Växande cosinus	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Ruttnande sinus	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Förfallande cosinus	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Delta-funktion	5 ( t )	1
Försenat delta	5 ( ta )	e ^-as

Egendomsnamn	Tidsdomänfunktion	Laplace-omvandling	Kommentar
	f ( t )	F ( s )
Linjäritet	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b är konstanta
Skalförändring	f ( at )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Flytta	e ^-at f ( t )	F ( s + a )
Dröjsmål	f ( ta )	e ^{- som} F ( s )
Härledning	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N: e härledningen	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Kraft	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integration	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Ömsesidig	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Veck	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* är konvolutionsoperatören
Periodisk funktion	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$