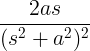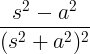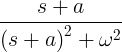లాప్లేస్ ట్రాన్స్ఫార్మ్

లాప్లేస్ ట్రాన్స్ఫార్మ్ సున్నా నుండి అనంతం వరకు ఏకీకరణ ద్వారా టైమ్ డొమైన్ ఫంక్షన్‌ను s- డొమైన్ ఫంక్షన్‌గా మారుస్తుంది

 టైమ్ డొమైన్ ఫంక్షన్, e -st చేత గుణించబడుతుంది .

అవకలన సమీకరణాలు మరియు సమగ్రాలకు త్వరగా పరిష్కారాలను కనుగొనడానికి లాప్లేస్ పరివర్తన ఉపయోగించబడుతుంది.

టైమ్ డొమైన్‌లో ఉత్పన్నం s- డొమైన్‌లో s ద్వారా గుణకారంగా మార్చబడుతుంది.

టైమ్ డొమైన్‌లో ఇంటిగ్రేషన్ s- డొమైన్‌లో s ద్వారా విభజనగా మార్చబడుతుంది.

లాప్లేస్ ట్రాన్స్ఫార్మ్ ఫంక్షన్

లాప్లేస్ పరివర్తన L }} ఆపరేటర్‌తో నిర్వచించబడింది :

F (లు) = \ mathcal {L} \ ఎడమ \ {f (t) \ కుడి \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt

విలోమ లాప్లేస్ పరివర్తన

విలోమ లాప్లేస్ పరివర్తనను నేరుగా లెక్కించవచ్చు.

సాధారణంగా విలోమ పరివర్తన పరివర్తన పట్టిక నుండి ఇవ్వబడుతుంది.

లాప్లేస్ ట్రాన్స్ఫార్మ్ టేబుల్

ఫంక్షన్ పేరు టైమ్ డొమైన్ ఫంక్షన్ లాప్లేస్ పరివర్తన

f ( టి )

F ( లు ) = L { f ( t )}
స్థిరంగా 1 \ frac {1} {s}
లీనియర్ t \ frac {1} {s ^ 2}
శక్తి

t n

\ frac {n!} {s ^ {n + 1}}
శక్తి

t a

Γ ( ఒక +1) ⋅ లు - ( ఒక +1)
ఘాతాంకం

ఇ వద్ద

\ frac {1} {sa}
సైన్

వద్ద పాపం

\ frac {a} {s ^ 2 + a ^ 2}
కొసైన్

వద్ద cos

\ frac {s} {s ^ 2 + a ^ 2}
హైపర్బోలిక్ సైన్

వద్ద sinh

\ frac {a} {s ^ 2-a ^ 2}
హైపర్బోలిక్ కొసైన్

వద్ద కోష్

\ frac {s} {s ^ 2-a ^ 2}
పెరుగుతున్న సైన్

t పాపం వద్ద

\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}
పెరుగుతున్న కొసైన్

t cos వద్ద

\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}
క్షీణిస్తున్న సైన్

e -at పాపం ωt

\ frac {\ ఒమేగా} {\ ఎడమ (s + a \ కుడి) ^ 2 + \ ఒమేగా ^ 2}
క్షీణించిన కొసైన్

e -at cos ωt

\ frac {s + a} {\ ఎడమ (s + a \ కుడి) ^ 2 + \ ఒమేగా ^ 2}
డెల్టా ఫంక్షన్

δ ( టి )

1

ఆలస్యం డెల్టా

δ ( టా )

e -as

లాప్లేస్ పరివర్తన లక్షణాలను

ఆస్తి పేరు టైమ్ డొమైన్ ఫంక్షన్ లాప్లేస్ పరివర్తన వ్యాఖ్య
 

f ( టి )

ఎఫ్ ( లు )

  
లీనియారిటీ af ( t ) + bg ( t ) aF ( లు ) + bG ( లు ) a , b స్థిరంగా ఉంటాయి
స్కేల్ మార్పు f ( వద్ద ) \ frac {1} {a} F \ ఎడమ (\ frac {s} {a} \ కుడి) a / 0
మార్పు e -at f ( t ) F ( s + a )  
ఆలస్యం f ( టా ) ఇ - వంటి F ( లు )  
ఉత్పన్నం \ frac {df (t)} {dt} sF ( లు ) - f (0)  
ఎన్-వ ఉత్పన్నం \ frac {d ^ nf (t)} {dt ^ n} s n f ( లు ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0)  
శక్తి t n f ( t ) (-1) ^ n \ frac {d ^ nF (లు)} {ds ^ n}  
అనుసంధానం \ int_ {0} ^ {t} f (x) dx \ frac {1} {s} F (లు)  
పరస్పరం \ frac {1} {t} f (t) \ int_ {s} ^ {\ infty} F (x) dx  
కన్వల్యూషన్ f ( t ) * g ( t ) F ( లు ) ⋅ G ( లు ) * కన్వల్యూషన్ ఆపరేటర్
ఆవర్తన ఫంక్షన్ f ( t ) = f ( t + T ) \ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx  

లాప్లేస్ పరివర్తన ఉదాహరణలు

ఉదాహరణ # 1

F (t) యొక్క పరివర్తనను కనుగొనండి:

f ( t ) = 3 t + 2 t 2

పరిష్కారం:

ℒ { t } = 1 / s 2

ℒ { t 2 } = 2 / s 3

F ( లు ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3

 

ఉదాహరణ # 2

F (ల) యొక్క విలోమ పరివర్తనను కనుగొనండి:

F ( లు ) = 3 / ( లు 2 + s - 6)

పరిష్కారం:

విలోమ పరివర్తనను కనుగొనడానికి, మేము s డొమైన్ ఫంక్షన్‌ను సరళమైన రూపానికి మార్చాలి:

F ( లు ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

A మరియు b లను కనుగొనడానికి, మనకు 2 సమీకరణాలు లభిస్తాయి - s గుణకాలలో ఒకటి మరియు మిగిలిన వాటిలో రెండవది:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, బి = -3/5

F ( లు ) = 3/5 ( లు -2) - 3/5 ( లు +3)

ఘాతాంక ఫంక్షన్ కోసం ట్రాన్స్ఫార్మ్స్ పట్టికను ఉపయోగించడం ద్వారా ఇప్పుడు F (లు) సులభంగా మార్చవచ్చు:

f ( t ) = (3/5) e 2 t - (3/5) e -3 t

 

ఇది కూడ చూడు

Advertising

కాలిక్యులస్
రాపిడ్ టేబుల్స్