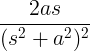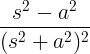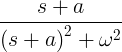Laplace Dönüşümü
- Laplace dönüşümü işlevi
- Laplace dönüşüm tablosu
- Laplace dönüşümü özellikleri
- Laplace dönüşümü örnekleri
Laplace dönüşümü, sıfırdan sonsuza entegrasyon yoluyla bir zaman etki alanı işlevini s etki alanı işlevine dönüştürür
e- st ile çarpılan zaman alanı işlevi .
Laplace dönüşümü, diferansiyel denklemler ve integraller için hızlı çözümler bulmak için kullanılır.
Zaman alanındaki türetme, s-alanındaki s ile çarpmaya dönüştürülür.
Zaman alanındaki entegrasyon, s-alanındaki s'ye bölünmeye dönüştürülür.
Laplace dönüşümü işlevi
Laplace dönüşümü, L {} operatörüyle tanımlanır :
![]()
Ters Laplace dönüşümü
Ters Laplace dönüşümü doğrudan hesaplanabilir.
Genellikle ters dönüşüm, dönüşümler tablosundan verilir.
Laplace dönüşüm tablosu
| Fonksiyon adı | Zaman alanı işlevi | Laplace dönüşümü |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Sabit | 1 | |
| Doğrusal | t | |
| Güç | t n |
|
| Güç | t bir |
Γ ( bir +1) ⋅ s - ( bir +1) |
| Üs | e at |
|
| Sinüs | sin de |
|
| Kosinüs | çünkü en |
|
| Hiperbolik sinüs |
SİNH de |
|
| Hiperbolik kosinüs |
cosh at |
|
| Büyüyen sinüs |
t sin de |
|
| Büyüyen kosinüs |
t , çünkü en |
|
| Çürüyen sinüs |
E -en sin ωt |
|
| Bozulan kosinüs |
e -at çünkü ωt |
|
| Delta işlevi |
δ ( t ) |
1 |
| Gecikmiş delta |
δ ( ta ) |
e -olarak |
Laplace dönüşümü özellikleri
| Mülkiyet adı | Zaman alanı işlevi | Laplace dönüşümü | Yorum Yap |
|---|---|---|---|
f ( t ) |
F ( ler ) |
||
| Doğrusallık | af ( t ) + bg ( t ) | aF ( ler ) + bG ( ler ) | a , b sabittir |
| Ölçek değişikliği | f ( içinde ) |
|
a / 0 |
| Vardiya | e -at f ( t ) | F ( s + a ) | |
| Gecikme | f ( ta ) | E - olarak F ( s ) | |
| Türetme |
|
sF ( ler ) - f (0) | |
| N. türetme |
|
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Güç | t n f ( t ) |
|
|
| Entegrasyon |
|
|
|
| Karşılıklı |
|
|
|
| Evrişim | f ( t ) * g ( t ) | F ( ler ) ⋅ G ( ler ) | * evrişim operatörüdür |
| Periyodik fonksiyon | f ( t ) = f ( t + T ) |
|
Laplace dönüşümü örnekleri
Örnek 1
F (t) 'nin dönüşümünü bulun:
f ( t ) = 3 t + 2 t 2
Çözüm:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Örnek 2
F (s) 'nin ters dönüşümünü bulun:
F ( s ) = 3 / ( s 2 + s - 6)
Çözüm:
Ters dönüşümü bulmak için s etki alanı işlevini daha basit bir biçime dönüştürmemiz gerekir:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
A ve b'yi bulmak için 2 denklem elde ederiz - biri s katsayıları ve ikincisi:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Artık F (ler) üs işlevi için dönüşüm tablosu kullanılarak kolayca dönüştürülebilir:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Ayrıca bakınız
Advertising
HESAP
- Sınırı
- Türev
- İntegral
- Dizi
- Laplace dönüşümü
- Evrişim
- Kalkülüs sembolleri
HIZLI TABLOLAR