معیاری انحراف

احتمال اور اعدادوشمار میں ، بے ترتیب متغیر کی معیاری انحراف معنی قدر سے بے ترتیب متغیر کا اوسط فاصلہ ہے۔

یہ نمائندگی کرتا ہے کہ کس طرح بے ترتیب متغیر کو اوسط قیمت کے قریب تقسیم کیا جاتا ہے۔ چھوٹا معیاری انحراف اشارہ کرتا ہے کہ بے ترتیب متغیر اوسط قیمت کے قریب تقسیم کیا جاتا ہے۔ بڑے پیمانے پر انحراف اس بات کی نشاندہی کرتا ہے کہ بے ترتیب متغیر اوسط قیمت سے بہت زیادہ تقسیم ہوتا ہے۔

معیاری انحراف کی تعریف کا فارمولا

معیاری انحراف rand کی اوسط قیمت کے ساتھ ، بے ترتیب متغیر X کے فرق کا مربع جڑ ہے۔

$ig سگما = ایس ٹی ڈی (ایکس) = \ اسکوائرٹ {ور (ایکس)} = q اسکرٹ {ای ((ایکس - ایم یو) ^ 2$

معیاری انحراف کی تعریف سے جو ہم حاصل کرسکتے ہیں

$ig سگما = ایس ٹی ڈی (ایکس) = q اسکرٹ {ای (ایکس ^ 2) - \ م ^ 2}$

مسلسل بے ترتیب متغیر کا معیاری انحراف

اوسط قیمت with اور امکانی کثافت تقریب f (x) کے ساتھ مستقل بے ترتیب متغیر کے ل::

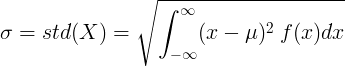
$ig سگما = ایس ٹی ڈی (ایکس) = \ اسکوائرٹ \ \ انٹ _ {- \ انفٹی} {{\ انفٹی} (x- \ mu) ^ 2 \: f (x) dx}$

یا

$ig سگما = ایس ٹی ڈی (ایکس) = \ اسکرٹ {\ بائیں [\ انٹ _ _ {- ty انفٹی} ^ {\ انفٹی} ایکس ^ 2 \: ایف (ایکس) ڈی ایکس \ دائیں] - \ میو ^ 2}$

مجرد بے ترتیب متغیر کا معیاری انحراف

متوازن بے ترتیب متغیر X کے لئے جس کی قدر μ اور امکانی بڑے پیمانے پر P (x) ہو:

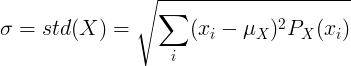
$ig سگما = ایس ٹی ڈی (ایکس) = \ اسکرٹ {\ سم_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}$

یا

$ig سگما = ایس ٹی ڈی (ایکس) = \ اسکرٹ {\ بائیں [\ خلاص_ {i} ^ {_ x_i ^ 2P (x_i) \ دائیں] - \ mu ^ 2}$

احتمال کی تقسیم ►

معیاری انحراف