توزيع الاحتمالات
في التوزيع الاحتمالي والإحصائي هو سمة لمتغير عشوائي ، يصف احتمالية المتغير العشوائي في كل قيمة.
لكل توزيع دالة كثافة احتمالية معينة ودالة توزيع احتمالية.
على الرغم من وجود عدد غير محدد من التوزيعات الاحتمالية ، إلا أن هناك العديد من التوزيعات الشائعة قيد الاستخدام.
دالة التوزيع التراكمي
يتم وصف التوزيع الاحتمالي بواسطة دالة التوزيع التراكمي F (x) ،
وهو احتمال المتغير العشوائي X للحصول على قيمة أصغر من أو تساوي x:
و ( س ) = ف ( س ≤ س )
التوزيع المستمر
يتم حساب دالة التوزيع التراكمي F (x) عن طريق تكامل دالة كثافة الاحتمال f (u) للمتغير العشوائي المستمر X.
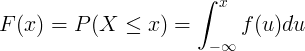
توزيع منفصل
يتم حساب دالة التوزيع التراكمي F (x) بجمع دالة الكتلة الاحتمالية P (u) للمتغير العشوائي المنفصل X.
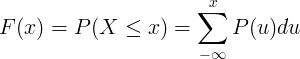
جدول التوزيعات المستمرة
التوزيع المستمر هو توزيع متغير عشوائي مستمر.
مثال التوزيع المستمر
...
جدول التوزيعات المستمرة
| اسم التوزيع | رمز التوزيع | دالة كثافة الاحتمال (pdf) | يعني | فرق |
|---|---|---|---|---|
|
و X ( س ) |
μ = E ( X ) |
σ 2 = فار ( X ) |
||
| عادي / غاوسي |
X ~ N (μ، σ 2 ) |
|
μ | σ 2 |
| زى موحد |
X ~ U ( أ ، ب ) |
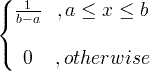 |
|
|
| متسارع | X ~ إكسب (λ) |
|
|
|
| جاما | س ~ جاما ( ج ، λ) |
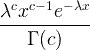 x / 0 ، c / 0 ، λ/ 0 |
|
|
| مربع تشي |
X ~ χ 2 ( ك ) |
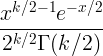 |
ك |
2 ك |
| ويشارت | ||||
| F |
X ~ F ( ك 1 ، ك 2 ) |
|||
| بيتا | ||||
| ويبل | ||||
| سجل عادي |
X ~ LN (μ، σ 2 ) |
|||
| رايلي | ||||
| كوشي | ||||
| ديريتشليت | ||||
| لابلاس | ||||
| الجبايه | ||||
| أرز | ||||
| الطالب t |
جدول التوزيعات المنفصلة
التوزيع المنفصل هو توزيع متغير عشوائي منفصل.
مثال التوزيع المنفصل
...
جدول التوزيعات المنفصلة
| اسم التوزيع | رمز التوزيع | دالة الكتلة الاحتمالية (pmf) | يعني | فرق | |
|---|---|---|---|---|---|
|
و س ( ك ) = ف ( س = ك ) ك = 0،1،2 ، ... |
ه ( س ) | فار ( x ) | |||
| ذات الحدين |
X ~ Bin ( n ، p ) |
|
np |
np (1- ع ) |
|
| بواسون |
X ~ بواسون (λ) |
|
λ ≥ 0 |
λ |
λ |
| زى موحد |
X ~ U ( أ ، ب ) |
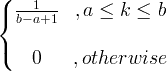 |
|
|
|
| هندسي |
X ~ Geom ( ع ) |
|
|
|
|
| فرط هندسي |
X ~ HG ( N ، K ، ن ) |
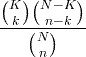 |
ن = 0،1،2 ، ... ك = 0،1 ، .. ، ن ن = 0،1 ، ... ، ن |
|
|
| برنولي |
X ~ برن ( ع ) |
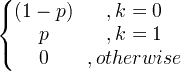 |
ص |
ص (1- ع ) |
|
أنظر أيضا
Advertising
الاحتمالات والإحصاءات
جداول سريعة