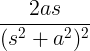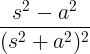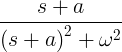Трансформация на Лаплас

Лапласовата трансформация преобразува функция от времева област в s-домейн функция чрез интегриране от нула до безкрайност

на функцията на времевия домейн, умножена по e ^-st .

Трансформацията на Лаплас се използва за бързо намиране на решения за диференциални уравнения и интеграли.

Деривацията във временната област се трансформира в умножение по s в s-домейна.

Интеграцията във времевия домейн се трансформира в разделяне на s в s-домейна.

Функция за преобразуване на Лаплас

Трансформацията на Лаплас се дефинира с оператора L {}:

$F (s) = \ mathcal {L} \ ляво \ {f (t) \ дясно \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Обратното преобразуване на Лаплас може да бъде изчислено директно.

Обикновено обратното преобразуване се дава от таблицата за преобразувания.

Име на функцията	Функция във времевия домейн	Лапласова трансформация
Име на функцията	f ( t )	F ( s ) = L { f ( t )}
Постоянно	1	$\ frac {1} {s}$
Линейна	t	$\ frac {1} {s ^ 2}$
Мощност	т ^н	$\ frac {n!} {s ^ {n + 1}}$
Мощност	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Експонента	д ^на	$\ frac {1} {sa}$
Синус	грях в	$\ frac {a} {s ^ 2 + a ^ 2}$
Косинус	защото при	$\ frac {s} {s ^ 2 + a ^ 2}$
Хиперболичен синус	sinh at	$\ frac {a} {s ^ 2-a ^ 2}$
Хиперболичен косинус	кош при	$\ frac {s} {s ^ 2-a ^ 2}$
Отглеждане на синус	т греши в	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Нарастващ косинус	t cos при	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Разлагащ се синус	e ^-at sin ωt	$\ frac {\ omega} {\ ляво (s + a \ дясно) ^ 2 + \ omega ^ 2}$
Разлагащ се косинус	e ^-at cos ωt	$\ frac {s + a} {\ ляво (s + a \ дясно) ^ 2 + \ omega ^ 2}$
Делта функция	δ ( t )	1
Забавена делта	δ ( ta )	e ^-as

Име на собственост	Функция във времевия домейн	Лапласова трансформация	Коментирайте
	f ( t )	F ( и )
Линейност	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b са постоянни
Промяна на мащаба	е ( при )	$\ frac {1} {a} F \ ляво (\ frac {s} {a} \ дясно)$	a / 0
Shift	e ^-at f ( t )	F ( s + a )
Забавяне	е ( та )	e ^{- като} F ( s )
Деривация	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-та деривация	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Мощност	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Интеграция	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} Ж (и)$
Взаимно	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Сгъване	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* е операторът на конволюцията
Периодична функция	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$