Функция Arccos (x)
Arccos (x), cos -1 (x), обратна косинусова функция.
Определение на Arccos
Аркосинусът на x се дефинира като обратна косинусова функция на x, когато -1≤x≤1.
Когато косинусът на y е равен на x:
cos y = x
Тогава аркосинусът на x е равен на обратната косинусова функция на x, която е равна на y:
arccos x = cos -1 x = y
(Тук cos -1 x означава обратния косинус и не означава косинус в степен -1).
Пример
arccos 1 = cos -1 1 = 0 rad = 0 °
Графика на аркос
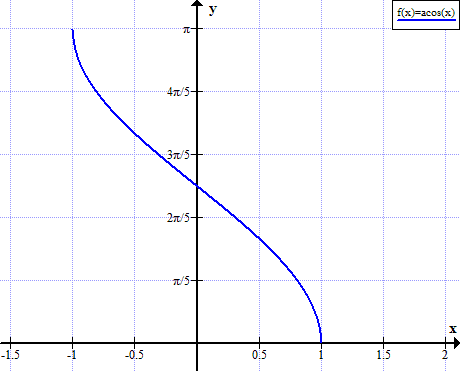
Правилата на Аркос
| Име на правилото | Правило |
|---|---|
| Косинус на аркозинус | cos (arccos x ) = x |
| Аркосинус от косинус | arccos (cos x ) = x + 2 k π, когато k ∈ℤ ( k е цяло число) |
| Arccos на отрицателен аргумент | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Допълнителни ъгли | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Сума на Arccos | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Аркос разлика | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos of sin of x | arccos (sin x ) = - x - (2 k +0.5) π |
| Синус на аркозинус |
|
| Тангенс на аркозина |
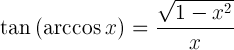 |
| Производно на аркозин |
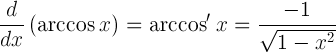 |
| Неопределен интеграл от аркозин |
|
Маса Arccos
| x | arccos (x) (рад) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Вижте също
- Функция косинус
- Функция Arcsine
- Арктанова функция
- Arccos калкулатор
- Преобразувател на радиани в градуси
- Аркос от 0
- Аркос от 1
- Аркос от 2
- Аркос от 3
- Arccos на cos
- Аркос на греха
- Производно на Arccos
- Графика на Arccos
- Cos на arccos
- Грехът на arccos
- Тен на аркос
Advertising
ТРИГОНОМЕТРИЯ
- Функция Arccos
- Функция Arcsin
- Арктанова функция
- Функция косинус
- Синусова функция
- Допирателна функция