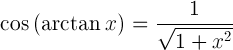Функция на арктангенс
Арктан (x), тен -1 (x), обратна допирателна функция.
Дефиниция на арктан
Арктангенсът на x се дефинира като обратната допирателна функция на x, когато x е действително (x ∈ℝ ).
Когато тангенсът на y е равен на x:
тен y = x
Тогава арктангенсът на x е равен на обратната допирателна функция на x, която е равна на y:
арктан х = тен -1 х = у
Пример
арктан 1 = тен -1 1 = π / 4 рад = 45 °
Графика на арктан
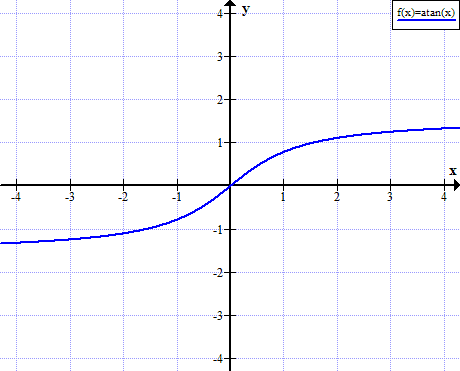
Прави арктан
| Име на правилото | Правило |
|---|---|
| Тангенс на арктангенса |
тен (арктан х ) = х |
| Арктан на отрицателен аргумент |
арктан (- х ) = - арктан х |
| Арктанова сума |
арктан α + арктан β = арктан [( α + β ) / (1- αβ )] |
| Арктанова разлика |
арктан α - арктан β = арктан [( α - β ) / (1+ αβ )] |
| Синус на арктангенс |
|
| Косинус от арктангенс |
|
| Взаимен аргумент |
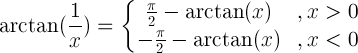 |
| Арктан от арксин |
|
| Производно на арктан |
|
| Неопределен интеграл от арктан |
|
Arctan маса
| x | арктан (x) (рад) |
арктан (x) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1,2490 | -71,565 ° |
| -2 | -1,1071 | -63.435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0,5 | -0,4636 | -26.565 ° |
| 0 | 0 | 0 ° |
| 0,5 | 0,4636 | 26.565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63.435 ° |
| 3 | 1,2490 | 71,565 ° |
| ∞ | π / 2 | 90 ° |
Вижте също
- Допирателна функция
- Функция на аркозинуса
- Функция Arcsine
- Арктан от 0
- Арктан от 1
- Арктан от 2
- Арктан на безкрайността
- Производно на арктан
- Интеграл на арктан
- Синус на арктан
- Косинус от арктан
- Арктанова графика
- Арктанов калкулатор
- Преобразувател в градуси в радиани
Advertising
ТРИГОНОМЕТРИЯ
- Функция Arccos
- Функция Arcsin
- Арктанова функция
- Функция косинус
- Синусова функция
- Допирателна функция
БЪРЗИ МАСИ