প্রাকৃতিক লোগারিদম - ln (x)

প্রাকৃতিক লোগারিদম হ'ল সংখ্যার বেস ইয়ের লোগারিথম।

প্রাকৃতিক লগারিদম সংজ্ঞা

কখন

e y = x

তারপরে x এর বেস ই লোগারিদম হয়

ln ( x ) = লগ ই ( এক্স ) = y

 

ই ধ্রুবক বা ইউলার সংখ্যা হল:

e ≈ 2.71828183

সূচকীয় ফাংশনের বিপরীত ফাংশন হিসাবে Ln

স্বাভাবিক লগারিদম ফাংশন LN (এক্স) -এর সূচকীয় ফাংশন ই বিপরীত ফাংশন এক্স ।

এক্স/ 0 এর জন্য

f ( f -1 ( x )) = e ln ( x ) = x

বা

f -1 ( f ( x )) = ln ( ই x ) = x

প্রাকৃতিক লোগারিদম বিধি এবং বৈশিষ্ট্য

বিধি নাম নিয়ম উদাহরণ
পণ্য বিধি

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + এলএন (7)
কোটারিয়েন্ট বিধি

ln ( x / y ) = ln ( x ) - ln ( y )

LN (3 / 7) = LN (3) - LN (7)
বিদ্যুৎ বিধি

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
ln ডেরিভেটিভ
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
ln অবিচ্ছেদ্য
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
নেতিবাচক সংখ্যা LN
 x ≤ 0 হলে ln ( x ) অপরিবর্তিত থাকে  
শূন্যের LN
 ln (0) অপরিশোধিত  
 
একের LN
 ln (1) = 0  
অনন্তের LN
 লিম ln ( x ) = ∞, যখন x → ∞ ∞  
ইউলারের পরিচয় ln (-1) = i π  

 

লোগারিদম পণ্য বিধি

X এবং y এর গুণনের লগারিদম হল x এর লোগারিদমের যোগফল এবং y এর লোগারিদমের সমষ্টি।

লগ বি ( x ∙ y ) = লগ বি ( এক্স ) + লগ বি ( y )

উদাহরণ স্বরূপ:

লগ 10 (3 ∙ 7) = লগ 10 (3) + লগ 10 (7)

লোগারিদম ভাগফলের নিয়ম

X এবং y এর বিভাজনের লগারিদম হ'ল x এর লোগারিদম এবং y এর লোগারিদমের পার্থক্য।

লগ বি ( x / y ) = লগ বি ( এক্স ) - লগ বি ( y )

উদাহরণ স্বরূপ:

লগ ইন করুন 10 (3 / 7) = log 10 (3) - লগ ইন করুন 10 (7)

লোগারিদম শক্তি বিধি

X এর লোগারিদম y এর ক্ষমতায় উত্থাপিত x এর লোগারিদমের y গুন।

লগ বি ( x y ) = y ∙ লগ বি ( এক্স )

উদাহরণ স্বরূপ:

লগ 10 (2 8 ) = 8 ∙ লগ 10 (2)

প্রাকৃতিক লোগারিদমের ডেরিভেটিভ

প্রাকৃতিক লোগারিদম ফাংশনের ডেরাইভেটিভ হ'ল পারস্পরিক ক্রিয়াকলাপ।

কখন

f ( x ) = ln ( x )

চ (এক্স) এর ডেরাইভেটিভ হ'ল:

f ' ( x ) = 1 / x

প্রাকৃতিক লোগারিদমের ইন্টিগ্রাল

প্রাকৃতিক লোগারিদম ফাংশনের অবিচ্ছেদ্য দ্বারা প্রদত্ত:

কখন

f ( x ) = ln ( x )

F (x) এর অবিচ্ছেদ্য হ'ল:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

0 এর Ln

শূন্যের প্রাকৃতিক লোগারিদম অপরিজ্ঞাত:

ln (0) অপরিশোধিত

X এর প্রাকৃতিক লোগারিদমের 0 এর কাছাকাছি সীমা, যখন x শূন্যের নিকটে আসে, বিয়োগ অনন্ত:

Ln এর 1

একের প্রাকৃতিক লোগারিদম শূন্য:

ln (1) = 0

অনন্তের Ln

অসীমের প্রাকৃতিক লোগারিদমের সীমা, যখন এক্স অনন্তের কাছে পৌঁছে যায়:

লিম ln ( x ) = ∞, যখন x → ∞ ∞

জটিল লগারিদম

জটিল সংখ্যা z এর জন্য:

z = re iθ = x + iy

জটিল লোগারিদম হবে (n = ...- 2, -1,0,1,2, ...):

লগ z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · আর্টিকান ( y / x ))

এলএন এর গ্রাফ (এক্স)

ln (x) x এর বাস্তব অ-ধনাত্মক মানের জন্য সংজ্ঞায়িত করা হয়নি:

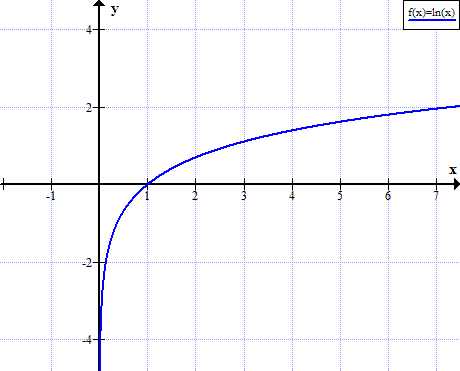
প্রাকৃতিক লোগারিথস টেবিল

এক্স ln x
0 অপরিবর্তিত
0 + - ∞
0.0001 -9.210340
0.001 -6.907755
0.01 -4.605170
0.1 -2.302585
1 0
2 0.693147
ই ≈ 2.7183 1
3 1.098612
4 1.386294
5 1.609438
6 1.791759
7 1.945910
8 2.079442
9 2.197225
10 2.302585
20 2.995732
30 3.401197
40 3.688879
50 3.912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4.605170
200 5.298317
300 5.703782
400 5.991465
500 6.214608
600 6.396930
700 6.551080
800 6.684612
900 6.802395
1000 6.907755
10000 9.210340

 

লগারিদম বিধি ►

 

আরো দেখুন

Advertising

ALGEBRA
দ্রুত টেবিল