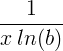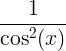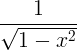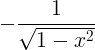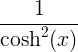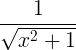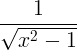ডেরিভেটিভ বিধি

ডেরাইভেটিভ বিধি এবং আইন। ফাংশন সারণির ডেরাইভেটিভস।

ডেরিভেটিভ সংজ্ঞা

একটি ফাংশনের ডেরাইভেটিভ হ'ল x + pointsx এবং x এর সাথে x এর বিন্দুতে ফাংশন মান f (x) এর পার্থক্যের অনুপাত, যখন infx অনন্যতম ছোট হয়। ডেরাইভেটিভ হ'ল বিন্দু x এ স্পর্শক রেখার ফাংশন opeাল বা opeাল।

 

f '(x) = \ lim _ {\ ডেল্টা x \ থেকে 0} \ frac {f (x + \ ডেল্টা x) -f (x)} {\ ডেল্টা এক্স}

দ্বিতীয় ডেরাইভেটিভ

দ্বিতীয় ডেরাইভেটিভ দিয়েছেন:

অথবা সহজভাবে প্রথম উপার্জনটি গ্রহণ করুন:

f '' (x) = (f '(x))'

নবম ডেরিভেটিভ

এন ম ব্যুৎপন্ন চ (x) এর এন বার আহরিত দ্বারা গণনা করা হয়।

এন ম ব্যুৎপন্ন হয় (ঢ -1) ব্যুৎপন্ন ব্যুৎপন্ন করার সমান:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

উদাহরণ:

এর চতুর্থ ডেরাইভেটিভ সন্ধান করুন

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

ফাংশনের গ্রাফে ডেরাইভেটিভ

ফাংশনের ডেরাইভেটিভ হ'ল স্পর্শকাতর রেখার opালু।

ডেরিভেটিভ বিধি

ডেরিভেটিভ যোগ বিধি

( আফ ( এক্স ) + বিজি ( এক্স )) '= আফ' ( এক্স ) + বিজি ' ( এক্স )
ডেরাইভেটিভ পণ্য বিধি

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
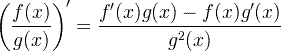ডেরিভেটিভ কোটেন্ট রুল \ বাম (\ frac {f (x)} {g (x)} \ ডান) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( এক্স)}
ডেরিভেটিভ চেইন বিধি

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

ডেরিভেটিভ যোগ বিধি

যখন ক এবং খ স্থির হয়।

( আফ ( এক্স ) + বিজি ( এক্স )) '= আফ' ( এক্স ) + বিজি ' ( এক্স )

উদাহরণ:

এর ডেরাইভেটিভ খুঁজুন:

3 এক্স 2 + 4 এক্স।

যোগফলের বিধি অনুসারে:

a = 3, খ = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 এক্স + 4

ডেরাইভেটিভ পণ্য বিধি

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

ডেরিভেটিভ কোটেন্ট রুল

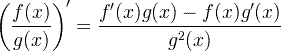
\ বাম (\ frac {f (x)} {g (x)} \ ডান) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( এক্স)}

ডেরিভেটিভ চেইন বিধি

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

এই নিয়মটি ল্যাঞ্জ্রেজের স্বরলিপি দিয়ে আরও ভালভাবে বোঝা যায়:

rac frac {df} {dx} = \ frac {df} g dg} d cdot \ frac {dg} {dx}

কার্য লিনিয়ার আনুমানিক

ছোট Δx এর জন্য, আমরা f (x 0 + Δx) এর একটি অনুমান পেতে পারি , যখন আমরা f (x 0 ) এবং f '(x 0 ) জানি:

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

ফাংশন সারণির ডেরাইভেটিভস

ফাংশন নাম ফাংশন অমৌলিক

চ ( এক্স )

 f '( x )
ধ্রুবক

কনস্ট

0

লিনিয়ার

এক্স

1

শক্তি

x ক

কুড়াল a- 1
ঘৃণ্য

ই x

ই x
ঘৃণ্য

একটি এক্স

a x ln a
প্রাকৃতিক লোগারিদম

এলএন ( এক্স )

লোগারিদম

লগ বি ( এক্স )

সাইন

পাপ এক্স

cos x
কোসিন

cos x

-সিন x
স্পর্শকাতর

ট্যান এক্স

আরকসিন

আরকসিন এক্স

আরকোসিন

আরকিওস এক্স

আর্কট্যানজেন্ট

আর্টিকান এক্স
হাইপারবোলিক সাইন

sinh x

কোশ এক্স
হাইপারবোলিক কোসাইন

কোশ এক্স

sinh x
হাইপারবোলিক স্পর্শক

তানহ x

বিপরীত হাইপারবারিক সাইন

sinh -1 x

বিপরীত হাইপারবোলিক কোসাইন

কোশ -1 এক্স

বিপরীত হাইপারবারিক স্পর্শক

তানহ -১ এক্স

উদ্দীপনা উদাহরণ

উদাহরণ # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

উদাহরণ # 2

f ( x ) = sin (3 x 2 )

চেইন বিধি প্রয়োগ করার সময়:

f ' ( x ) = কোস (3 x 2 ) ⋅ [3 x 2 ]' = কোস (3 এক্স 2 ) ⋅ 6 এক্স

দ্বিতীয় ডেরিভেটিভ পরীক্ষা

যখন কোনও ফাংশনের প্রথম ডেরাইভেটিভ x 0 বিন্দুতে শূন্য হয় ।

f '( x 0 ) = 0

তারপরে x 0 , f '' (x 0 ) এর দ্বিতীয় ডেরাইভেটিভ, বিন্দুর প্রকারটি নির্দেশ করতে পারে:

 

f '' ( x 0 )/ 0

 স্থানীয় সর্বনিম্ন

f '' ( x 0 ) <0

 স্থানীয় সর্বাধিক

f '' ( x 0 ) = 0

 নির্ধারিত

 

আরো দেখুন

Advertising

ক্যালকুলাস
দ্রুত টেবিল