Distribució de la probabilitat

En probabilitat i estadística la distribució és una característica d'una variable aleatòria, descriu la probabilitat de la variable aleatòria en cada valor.

Cada distribució té una determinada funció de densitat de probabilitat i funció de distribució de probabilitats.

Tot i que hi ha un nombre indefinit de distribucions de probabilitat, hi ha diverses distribucions comunes en ús.

Funció de distribució acumulativa

La distribució de probabilitat es descriu mitjançant la funció de distribució acumulada F (x),

que és la probabilitat que la variable aleatòria X obtingui un valor menor o igual a x:

F ( x ) = P ( X ≤ x )

Distribució contínua

La funció de distribució acumulativa F (x) es calcula integrant la funció de densitat de probabilitat f (u) de la variable aleatòria contínua X.

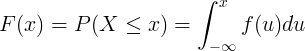
Distribució discreta

La funció de distribució acumulativa F (x) es calcula sumant la funció de massa de probabilitat P (u) de la variable aleatòria discreta X.

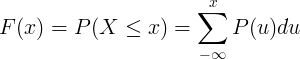
Taula de distribucions contínues

La distribució contínua és la distribució d’una variable aleatòria contínua.

Exemple de distribució contínua

...

Taula de distribucions contínues

Nom de la distribució Símbol de distribució Funció de densitat de probabilitat (pdf) Significar Desacord
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussià

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniforme

X ~ U ( a , b )

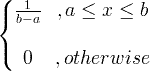 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, en cas contrari \ end {matrix} \ frac {(ba) ^ 2} {12}
Exponencial X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
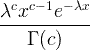Gamma X ~ gamma ( c , λ) \ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Plaça Chi

X ~ χ 2 ( k )

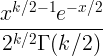 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Registre normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Levy        
Arròs        
Estudiant t        

Taula de distribucions discretes

La distribució discreta és la distribució d’una variable aleatòria discreta.

Exemple de distribució discreta

...

Taula de distribucions discretes

Nom de la distribució Símbol de distribució Funció de massa de probabilitat (pmf) Significar Desacord
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binomi

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniforme

X ~ U ( a, b )

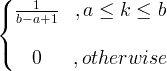 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, en cas contrari \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geomètrica

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hipergeomètric

X ~ HG ( N , K , n )

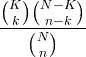N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Berna ( p )

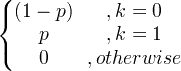 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, en cas contrari \ end {matrix}

p

p (1- p )

 

Vegeu també

Advertising

PROBABILITAT I ESTADÍSTICA
TAULES RÀPIDES