Desviació estàndar

En probabilitat i estadístiques, la desviació estàndard d'una variable aleatòria és la distància mitjana d'una variable aleatòria del valor mitjà.

Representa com es distribueix la variable aleatòria prop del valor mitjà. Una petita desviació estàndard indica que la variable aleatòria es distribueix a prop del valor mitjà. La gran desviació estàndard indica que la variable aleatòria es distribueix lluny del valor mitjà.

Fórmula de definició de desviació estàndard

La desviació estàndard és l’arrel quadrada de la variància de la variable aleatòria X, amb un valor mitjà de μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

A partir de la definició de la desviació estàndard que podem obtenir

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Desviació estàndard de la variable aleatòria contínua

Per a variables aleatòries contínues amb valor mitjà μ i funció de densitat de probabilitat f (x):

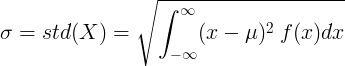
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

o

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Desviació estàndard de la variable aleatòria discreta

Per a la variable aleatòria discreta X amb valor mitjà μ i funció de massa de probabilitat P (x):

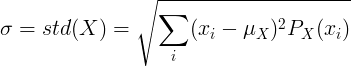
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

o

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Distribució de la probabilitat ►

 

Vegeu també

Advertising

PROBABILITAT I ESTADÍSTICA
TAULES RÀPIDES