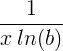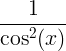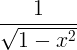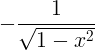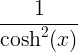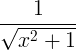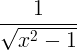Ableitungsregeln

Abgeleitete Regeln und Gesetze. Ableitungen der Funktionstabelle.

Abgeleitete Definition

Die Ableitung einer Funktion ist das Verhältnis der Differenz des Funktionswerts f (x) an den Punkten x + Δx und x zu Δx, wenn Δx unendlich klein ist. Die Ableitung ist die Funktionssteigung oder Steigung der Tangentenlinie am Punkt x.

 

f '(x) = \ lim _ {\ Delta x \ bis 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

Zweite Ableitung

Die zweite Ableitung ist gegeben durch:

Oder leiten Sie einfach die erste Ableitung ab:

f '' (x) = (f '(x))'

N-te Ableitung

Die n- te Ableitung wird berechnet, indem f (x) n-mal abgeleitet wird.

Die n- te Ableitung ist gleich der Ableitung der (n-1) -Derivat:

f ( n ) ( x ) = [ f ( n & supmin ; ¹) ( x )] '

Beispiel:

Finden Sie die vierte Ableitung von

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

Ableitung auf Funktionsgraph

Die Ableitung einer Funktion ist die Steigung der Tangentiallinie.

Ableitungsregeln

Ableitungssummenregel

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Derivative Produktregel

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
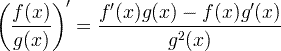Abgeleitete Quotientenregel \ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
Ableitungskettenregel

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Ableitungssummenregel

Wenn a und b Konstanten sind.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Beispiel:

Finden Sie die Ableitung von:

3 x 2 + 4 x.

Nach der Summenregel:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Derivative Produktregel

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Abgeleitete Quotientenregel

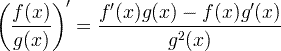
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

Ableitungskettenregel

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Diese Regel kann mit Lagranges Notation besser verstanden werden:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Funktion lineare Approximation

Für kleines Δx können wir eine Annäherung an f (x 0 + Δx) erhalten, wenn wir f (x 0 ) und f '(x 0 ) kennen:

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

Ableitungen der Funktionstabelle

Funktionsname Funktion Derivat

f ( x )

 f '( x )
Konstante

const

0

Linear

x

1

Leistung

x a

Axt a- 1
Exponentiell

e x

e x
Exponentiell

a x

a x ln a
Natürlicher Logarithmus

ln ( x )

Logarithmus

log b ( x )

Sinus

sin x

cos x
Kosinus

cos x

-sin x
Tangente

tan x

Arcsine

arcsin x

Arccosin

Arccos x

Arctangent

arctan x
Hyperbolischer Sinus

sinh x

cosh x
Hyperbolischer Kosinus

cosh x

sinh x
Hyperbolische Tangente

tanh x

Inverser hyperbolischer Sinus

sinh -1 x

Inverser hyperbolischer Kosinus

cosh -1 x

Inverse hyperbolische Tangente

tanh -1 x

Abgeleitete Beispiele

Beispiel 1

f ( x ) = x 3 + 5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 + 10 x +1

Beispiel 2

f ( x ) = sin (3 x 2 )

Bei Anwendung der Kettenregel:

f ' ( x ) = cos (3 x 2 ) ≤ [3 x 2 ]' = cos (3 x 2 ) ≤ 6 x

Test der zweiten Ableitung

Wenn die erste Ableitung einer Funktion am Punkt x 0 Null ist .

f '( x 0 ) = 0

Dann kann die zweite Ableitung am Punkt x 0 , f '' (x 0 ), den Typ dieses Punktes angeben:

 

f '' ( x 0 )/ 0

 lokales Minimum

f '' ( x 0 ) <0

 lokales Maximum

f '' ( x 0 ) = 0

 unbestimmt

 

Siehe auch

Advertising

INFINITESIMALRECHNUNG
SCHNELLE TABELLEN