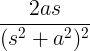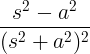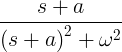Laplace-Transformation

Die Laplace-Transformation konvertiert eine Zeitdomänenfunktion durch Integration von Null nach Unendlich in eine S-Domänenfunktion

der Zeitbereichsfunktion, multipliziert mit e- ^st .

Die Laplace-Transformation wird verwendet, um schnell Lösungen für Differentialgleichungen und Integrale zu finden.

Die Ableitung im Zeitbereich wird in die Multiplikation mit s im s-Bereich umgewandelt.

Die Integration in die Zeitdomäne wird in eine Division durch s in der S-Domäne umgewandelt.

Laplace-Transformationsfunktion

Die Laplace-Transformation wird mit dem Operator L {} definiert :

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Die inverse Laplace-Transformation kann direkt berechnet werden.

Normalerweise wird die inverse Transformation aus der Transformationstabelle angegeben.

Funktionsname	Zeitbereichsfunktion	Laplace-Transformation
Funktionsname	f ( t )	F ( s ) = L { f ( t )}
Konstante	1	$\ frac {1} {s}$
Linear	t	$\ frac {1} {s ^ 2}$
Leistung	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Leistung	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Exponent	e ^at	$\ frac {1} {sa}$
Sinus	Sünde an	$\ frac {a} {s ^ 2 + a ^ 2}$
Kosinus	cos bei	$\ frac {s} {s ^ 2 + a ^ 2}$
Hyperbolischer Sinus	sinh bei	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolischer Kosinus	cosh at	$\ frac {s} {s ^ 2-a ^ 2}$
Wachsender Sinus	t sündigen bei	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Wachsender Kosinus	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Verfallender Sinus	e ^-at sin wt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Verfallender Kosinus	e ^-at cos wt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Delta-Funktion	δ ( t )	1
Verzögertes Delta	δ ( ta )	e ^-as

Name des Anwesens	Zeitbereichsfunktion	Laplace-Transformation	Kommentar
	f ( t )	F ( s )
Linearität	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b sind konstant
Skalenänderung	f ( at )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Verschiebung	e- ^at f ( t )	F ( s + a )
Verzögern	f ( ta )	e ^{- als} F ( s )
Ableitung	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-te Ableitung	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Leistung	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integration	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Gegenseitig	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Faltung	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* ist der Faltungsoperator
Periodische Funktion	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$