Convolution

La convolution est la fonction de corrélation de f (τ) avec la fonction inversée g (t-τ).

L'opérateur de convolution est le symbole astérisque * .

La convolution de f (t) et g (t) est égale à l'intégrale de f (τ) fois f (t-τ):

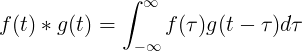
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

La convolution de 2 fonctions discrètes est définie comme:

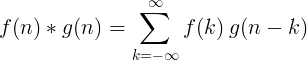
$f (n) * g (n) = \ somme_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

La convolution discrète bidimensionnelle est généralement utilisée pour le traitement d'image.

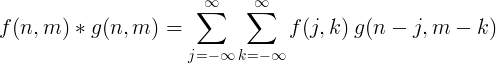
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

On peut filtrer le signal d'entrée discret x (n) par convolution avec la réponse impulsionnelle h (n) pour obtenir le signal de sortie y (n).

y ( n ) = x ( n ) * h ( n )

La transformée de Fourier d'une multiplication de 2 fonctions est égale à la convolution des transformées de Fourier de chaque fonction:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

La transformée de Fourier d'une convolution de 2 fonctions est égale à la multiplication des transformées de Fourier de chaque fonction:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Voir également