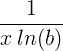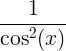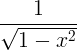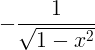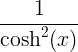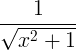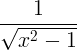Règles dérivées

Règles et lois dérivées. Tableau des dérivés des fonctions.

• Définition dérivée
• Règles dérivées
• Tableau des dérivés des fonctions
• Exemples dérivés

Définition dérivée

La dérivée d'une fonction est le rapport de la différence de valeur de fonction f (x) aux points x + Δx et x avec Δx, lorsque Δx est infiniment petit. La dérivée est la fonction pente ou pente de la ligne tangente au point x.

Second dérivé

La seconde dérivée est donnée par:

Ou dérivez simplement le premier dérivé:

Nième dérivé

La n ième dérivée est calculée en dérivant f (x) n fois.

Le n ième dérivé est égal au dérivé du dérivé (n-1):

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Exemple:

Trouvez le quatrième dérivé de

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]' = 240 x

Dérivée sur graphique de fonction

La dérivée d'une fonction est la pente de la ligne tangentielle.

Règles dérivées

Règle de somme dérivée	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Règle du produit dérivé	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Règle du quotient dérivé
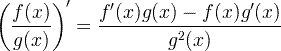Règle de chaîne dérivée	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Règle de somme dérivée

Quand a et b sont des constantes.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Exemple:

Trouvez le dérivé de:

3 x ² + 4 x.

Selon la règle de la somme:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Règle du produit dérivé

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Règle du quotient dérivé

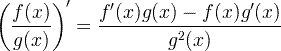
Règle de chaîne dérivée

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Cette règle peut être mieux comprise avec la notation de Lagrange:

Fonction d'approximation linéaire

Pour les petits Δx, on peut obtenir une approximation de f (x ₀ + Δx), quand on connaît f (x ₀ ) et f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Tableau des dérivés des fonctions

Nom de la fonction	Fonction	Dérivé
	f ( x )	f '( x )
Constant	const	0
Linéaire	x	1
Puissance	x a	hache a- 1
Exponentiel	e x	e x
Exponentiel	un x	a x ln a
Un algorithme naturel	ln ( x )
Logarithme	log b ( x )
Sinus	sin x	cos x
Cosinus	cos x	-sin x
Tangente	bronzage x
Arcsine	arcsin x
Arccosine	arccos x
Arc tangent	arctan x
Sinus hyperbolique	sinh x	cosh x
Cosinus hyperbolique	cosh x	sinh x
Tangente hyperbolique	tanh x
Sinus hyperbolique inverse	sinh -1 x
Cosinus hyperbolique inverse	cosh -1 x
Tangente hyperbolique inverse	tanh -1 x

Exemples dérivés

Exemple 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Exemple # 2

f ( x ) = sin (3 x ² )

Lors de l'application de la règle de chaîne:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Test dérivé secondaire

Lorsque la première dérivée d'une fonction est nulle au point x ₀ .

f '( x ₀ ) = 0

Alors la deuxième dérivée au point x ₀ , f '' (x ₀ ), peut indiquer le type de ce point:

Voir également

• Calcul
• Transformée de Laplace ( ℒ  )
• Symboles de calcul