संभावना वितरण
संभाव्यता और सांख्यिकी वितरण एक यादृच्छिक चर की विशेषता है, प्रत्येक मूल्य में यादृच्छिक चर की संभावना का वर्णन करता है।
प्रत्येक वितरण में एक निश्चित संभाव्यता घनत्व फ़ंक्शन और प्रायिकता वितरण फ़ंक्शन होता है।
हालांकि प्रायिकता वितरण की अनिश्चित संख्या है, लेकिन उपयोग में कई सामान्य वितरण हैं।
संचयी वितरण फलन
संभाव्यता वितरण को संचयी वितरण फ़ंक्शन F (x) द्वारा वर्णित किया गया है,
जो यादृच्छिक चर X की संभावना x के बराबर या उससे छोटे मान प्राप्त करने के लिए है:
एफ ( एक्स ) = पी ( एक्स ≤ एक्स )
निरंतर वितरण
संचयी वितरण फ़ंक्शन F (x) निरंतर यादृच्छिक चर X की प्रायिकता घनत्व फ़ंक्शन f (u) के एकीकरण द्वारा गणना की जाती है।
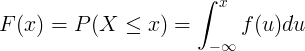
असतत वितरण
संचयी वितरण फ़ंक्शन F (x) की गणना असतत यादृच्छिक चर X के प्रायिकता मास फ़ंक्शन P (u) के योग से की जाती है।
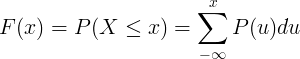
निरंतर वितरण तालिका
सतत वितरण एक सतत यादृच्छिक चर का वितरण है।
निरंतर वितरण उदाहरण
...
निरंतर वितरण तालिका
| वितरण नाम | वितरण का प्रतीक | संभाव्यता घनत्व फ़ंक्शन (पीडीएफ) | मीन | झगड़ा |
|---|---|---|---|---|
|
च X ( x ) |
μ = E ( X ) |
σ 2 = वार ( एक्स ) |
||
| सामान्य / गाऊसी |
एक्स ~ एन (μ, ) 2 ) |
|
μ | σ २ |
| वर्दी |
एक्स ~ यू ( ए , बी ) |
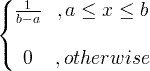 |
|
|
| घातीय | एक्स ~ ऍक्स्प (λ) |
|
|
|
| गामा | एक्स ~ गामा ( c , λ) |
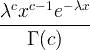 x / 0, c / 0, λ/ 0 |
|
|
| ची चौक |
X ~ χ 2 ( k ) |
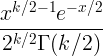 |
के |
2 के |
| विशार्ट | ||||
| एफ |
X ~ F ( k 1 , k 2 ) |
|||
| बीटा | ||||
| वेइबुल | ||||
| लॉग-सामान्य |
X ~ LN (μ, ) 2 ) |
|||
| रेले | ||||
| कॉची | ||||
| Dirichlet | ||||
| लाप्लास | ||||
| उगाही | ||||
| चावल | ||||
| विद्यार्थी का टी |
असतत वितरण तालिका
असतत वितरण एक असतत यादृच्छिक चर का वितरण है।
असतत वितरण उदाहरण
...
असतत वितरण तालिका
| वितरण नाम | वितरण का प्रतीक | संभाव्यता द्रव्यमान समारोह (pmf) | मीन | झगड़ा | |
|---|---|---|---|---|---|
|
f x ( k ) = P ( X = k ) k = 0,1,2, ... |
ई ( एक्स ) | वार ( x ) | |||
| द्विपद |
एक्स ~ बिन ( एन , पी ) |
|
एनपी |
एनपी (1- पी ) |
|
| प्वासों |
एक्स ~ पोइसन (λ) |
|
λ ≥ 0 |
λ |
λ |
| वर्दी |
एक्स ~ यू ( ए, बी ) |
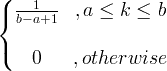 |
|
|
|
| ज्यामितिक |
एक्स ~ जीओएम ( पी ) |
|
|
|
|
| हाइपर-ज्यामितीय |
एक्स ~ एचजी ( एन , के , एन ) |
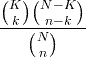 |
एन = 0,1,2, ... के = 0,1, .., एन n = 0,1, ..., एन |
|
|
| Bernoulli |
एक्स ~ बर्न ( पी ) |
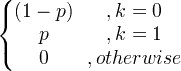 |
पी |
पी (1- पी ) |
|
यह सभी देखें
Advertising
संभावना और सांख्यिकी
रैपिड टाइलें