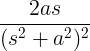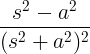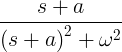Laplaceova transformacija
- Laplaceova funkcija transformacije
- Laplaceova tablica transformacije
- Svojstva Laplaceove transformacije
- Primjeri Laplaceove transformacije
Laplaceova transformacija pretvara funkciju vremenske domene u funkciju s-domene integracijom od nule do beskonačnosti
funkcije vremenske domene, pomnoženo s e -st .
Laplaceova transformacija koristi se za brzo pronalaženje rješenja za diferencijalne jednadžbe i integrale.
Izvođenje u vremenskoj domeni pretvara se u množenje s u s-domeni.
Integracija u vremenskoj domeni pretvara se u podjelu s u s-domeni.
Laplaceova funkcija transformacije
Laplaceova transformacija definirana je s operatorom L {}:
![]()
Inverzna Laplaceova transformacija
Inverzna Laplaceova transformacija može se izračunati izravno.
Obično se inverzna transformacija daje iz tablice transformacija.
Laplaceova tablica transformacije
| Naziv funkcije | Funkcija vremenske domene | Laplaceova transformacija |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Konstantno | 1 | |
| Linearno | t | |
| Vlast | t n |
|
| Vlast | t a |
Γ ( + 1) ⋅ s - ( + 1) |
| Eksponent | e u |
|
| Sinus | grijeh na |
|
| Kosinus | jer na |
|
| Hiperbolički sinus |
sinh at |
|
| Hiperbolički kosinus |
cosh na |
|
| Uzgoj sinusa |
t sin na |
|
| Raste kosinus |
t cos at |
|
| Propadajući sinus |
e -at sin ωt |
|
| Propadajući kosinus |
e -at cos ωt |
|
| Delta funkcija |
δ ( t ) |
1 |
| Odgođena delta |
δ ( ta ) |
e -as |
Svojstva Laplaceove transformacije
| Naziv nekretnine | Funkcija vremenske domene | Laplaceova transformacija | Komentar |
|---|---|---|---|
f ( t ) |
F ( e ) |
||
| Linearnost | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b su konstantne |
| Promjena ljestvice | f ( u ) |
|
a / 0 |
| Shift | e -at f ( t ) | F ( s + a ) | |
| Odgoditi | f ( ta ) | e - kao F ( s ) | |
| Izvođenje |
|
sF ( s ) - f (0) | |
| N-to izvođenje |
|
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Vlast | t n f ( t ) |
|
|
| Integracija |
|
|
|
| Recipročan |
|
|
|
| Konvolucija | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * je operator konvolucije |
| Povremena funkcija | f ( t ) = f ( t + T ) |
|
Primjeri Laplaceove transformacije
Primjer # 1
Pronađite transformaciju f (t):
f ( t ) = 3 t + 2 t 2
Riješenje:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Primjer # 2
Pronađite inverznu transformaciju F (s):
Ž ( s ) = 3 / ( s 2 + s - 6)
Riješenje:
Da bismo pronašli inverznu transformaciju, moramo promijeniti funkciju s domene u jednostavniji oblik:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Da bismo pronašli a i b, dobivamo 2 jednadžbe - jednu od s koeficijenata, a drugu od ostalih:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
Ž ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Sada se F (s) može lako transformirati pomoću tablice transformacija za funkciju eksponenta:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Vidi također
Advertising
RAČUN
- Ograničiti
- Izvedena
- Sastavni
- Niz
- Laplaceova transformacija
- Konvolucija
- Simboli računa
BRZE TABLICE