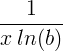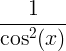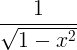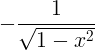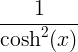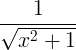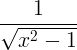Afleiðurreglur

Afleiddar reglur og lög. Afleiður aðgerða tafla.

• Afleiðuskilgreining
• Afleiðurreglur
• Afleiður aðgerða tafla
• Afleidd dæmi

Afleiðuskilgreining

Afleiða falls er hlutfall mismunur fallgildisins f (x) í punktum x + Δx og x við Δx, þegar Δx er óendanlega lítill. Afleiðan er fallhalli eða halli snertilínunnar við punkt x.

Önnur afleiða

Önnur afleiðan er gefin af:

Eða einfaldlega leiða fyrstu afleiðuna:

Nunda afleiða

The n Th afleiðan er reiknuð með því sem skapast vegna f (X) n sinnum.

The N Th afleiður er jafn stór og afleiða af sambandinu (n-1) afleiða:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Dæmi:

Finndu fjórðu afleiðuna af

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' [10 x ⁴ ] '' = [40 x ³ ] '' = [120 x ² ] '= 240 x

Afleiða á grafi um aðgerð

Afleiða falls er halla snertilínunnar.

Afleiðurreglur

Afleiðusumaregla	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Afleiðuvara regla	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Afleidd kvótaregla
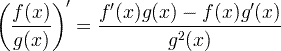Afleidd keðjuregla	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Afleiðusumaregla

Þegar a og b eru fastar.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Dæmi:

Finndu afleiðuna af:

3 x ² + 4 x.

Samkvæmt summureglunni:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Afleiðuvara regla

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Afleidd kvótaregla

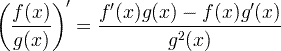
Afleidd keðjuregla

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Þessa reglu er hægt að skilja betur með táknun Lagrange:

Aðgerð línuleg nálgun

Fyrir lítið Δx getum við fengið nálgun við f (x ₀ + Δx), þegar við þekkjum f (x ₀ ) og f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Afleiður aðgerða tafla

Aðgerðarheiti	Virka	Afleiða
	f ( x )	f '( x )
Stöðugur	const	0
Línuleg	x	1
Kraftur	x a	öxi a- 1
Veldisvísir	e x	e x
Veldisvísir	a x	a x ln a
Náttúrulegur lógaritmi	ln ( x )
Logaritmi	log b ( x )
Sinus	synd x	cos x
Kósínus	cos x	-syndur x
Tangent	sólbrúnt x
Bogbogi	bogi x
Arccosine	arcoos x
Arctangent	arctan x
Siðblóðþrýstingur	sinh x	cosh x
Hyperbolic kósínus	cosh x	sinh x
Hyperbolic tangens	tanh x
Andhverfur hyperbolic sinus	sinh -1 x
Andhverft hyperbolískt kósínus	cosh -1 x
Andhverfur hyperbolic snerti	tanh -1 x

Afleidd dæmi

Dæmi # 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Dæmi # 2

f ( x ) = sin (3 x ² )

Þegar keðjureglan er notuð:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Annað afleiðupróf

Þegar fyrsta afleiðan af falli er núll í punktinum x ₀ .

f '( x ₀ ) = 0

Síðan getur önnur afleiðan í lið x ₀ , f '' (x ₀ ) gefið til kynna tegund þess punktar:

Sjá einnig

• Reiknivél
• Laplace umbreyting ( ℒ  )
• Reiknistákn