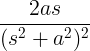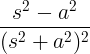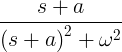Laplace Transform

Laplace umbreyting breytir tímalénsaðgerð í s-lénaðgerð með samþættingu frá núlli til óendanleika

^{tímalénaðgerðarinnar} , margfaldað með e ^-st .

Laplace umbreytingin er notuð til að finna fljótt lausnir fyrir mismunadreifi og heildarhluta.

Afleiðing í tímaléninu er umbreytt í margföldun með s í s-léninu.

Samþætting í tímaléninu er umbreytt í deilingu með s í s-léninu.

Laplace umbreytingaraðgerð

Laplace umbreytingin er skilgreind með L {} stjórnandanum:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Andhverfa Laplace umbreytinguna er hægt að reikna beint.

Venjulega er andhverfa umbreytingin gefin frá umbreytingartöflunni.

Aðgerðarheiti	Tímalén virka	Laplace umbreyting
Aðgerðarheiti	f ( t )	F ( s ) = L { f ( t )}
Stöðugur	1	$\ frac {1} {s}$
Línuleg	t	$\ frac {1} {s ^ 2}$
Kraftur	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Kraftur	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Veldisvígur	e ^kl	$\ frac {1} {sa}$
Sinus	syndga á	$\ frac {a} {s ^ 2 + a ^ 2}$
Kósínus	cos kl	$\ frac {s} {s ^ 2 + a ^ 2}$
Siðblóðþrýstingur	sinh kl	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolic kósínus	cosh kl	$\ frac {s} {s ^ 2-a ^ 2}$
Vaxandi sinus	t synda á	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Vaxandi kósínus	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Rotnandi sinus	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Rotnandi kósínus	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Delta virka	δ ( t )	1
Seinkað delta	δ ( ta )	e ^-as

Nafn eignar	Tímalén virka	Laplace umbreyting	Athugasemd
	f ( t )	F ( s )
Línulegt	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b eru stöðug
Stærðarbreyting	f ( at )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Vakt	e ^-at f ( t )	F ( s + a )
Seinkaðu	f ( ta )	e ^{- eins og} F ( s )
Afleiðing	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-afleiðsla	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Kraftur	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Samþætting	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Gagnkvæm	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Convolution	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* er kröftunaraðilinn
Regluleg virkni	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$