Sisihan piawai

Dalam kebarangkalian dan statistik, sisihan piawai bagi pemboleh ubah rawak adalah jarak purata pemboleh ubah rawak dari nilai min.

Ini menunjukkan bagaimana pemboleh ubah rawak diedarkan berhampiran nilai min. Sisihan piawai kecil menunjukkan bahawa pemboleh ubah rawak diedarkan berhampiran nilai min. Sisihan piawai besar menunjukkan bahawa pemboleh ubah rawak diedarkan jauh dari nilai min.

Formula definisi sisihan piawai

Sisihan piawai adalah punca kuasa dua varians pemboleh ubah rawak X, dengan nilai min μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Dari definisi sisihan piawai yang kita dapat

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Sisihan piawai pemboleh ubah rawak berterusan

Untuk pemboleh ubah rawak berterusan dengan nilai min μ dan fungsi ketumpatan kebarangkalian f (x):

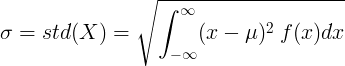
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

atau

\ sigma = std (X) = \ sqrt {\ kiri [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ kanan] - \ mu ^ 2}

Sisihan piawai pemboleh ubah rawak diskrit

Untuk pemboleh ubah rawak X diskrit dengan nilai min μ dan fungsi jisim kebarangkalian P (x):

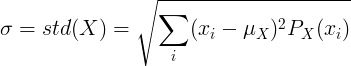
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

atau

\ sigma = std (X) = \ sqrt {\ kiri [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ kanan] - \ mu ^ 2}

 

Taburan kebarangkalian ►

 

Lihat juga

Advertising

KEBARANGKALIAN & STATISTIK
JADUAL RAPID