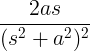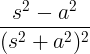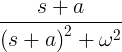Laplace Transform

Laplace-transform konverterer en tidsdomene-funksjon til s-domene-funksjon ved integrering fra null til uendelig

av tidsdomenefunksjonen, multiplisert med e ^-st .

Laplace-transformasjonen brukes til raskt å finne løsninger for differensialligninger og integraler.

Derivasjon i tidsdomenet transformeres til multiplikasjon med s i s-domene.

Integrasjon i tidsdomenet transformeres til divisjon av s i s-domene.

Laplace transform-funksjon

Laplace-transformasjonen er definert med L {} -operatøren:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Den omvendte Laplace-transformasjonen kan beregnes direkte.

Vanligvis er den omvendte transformasjonen gitt fra transformasjonstabellen.

Funksjonsnavn	Tidsdomenefunksjon	Laplace transform
Funksjonsnavn	f ( t )	F ( s ) = L { f ( t )}
Konstant	1	$\ frac {1} {s}$
Lineær	t	$\ frac {1} {s ^ 2}$
Makt	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Makt	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Eksponent	e ^kl	$\ frac {1} {sa}$
Sine	synd på	$\ frac {a} {s ^ 2 + a ^ 2}$
Cosine	cos kl	$\ frac {s} {s ^ 2 + a ^ 2}$
Hyperbolisk sinus	sinh kl	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolisk cosinus	kos på	$\ frac {s} {s ^ 2-a ^ 2}$
Voksende sinus	t synd på	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Voksende cosinus	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Råtnende sinus	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Råtnende cosinus	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Delta-funksjon	δ ( t )	1
Forsinket delta	δ ( ta )	e ^-as

Eiendomsnavn	Tidsdomenefunksjon	Laplace transform	Kommentar
	f ( t )	F ( s )
Lineæritet	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b er konstante
Skalaendring	f ( kl )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Skifte	e ^-at f ( t )	F ( s + a )
Forsinkelse	f ( ta )	e ^{- som} F ( s )
Derivasjon	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-avledning	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Makt	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integrering	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Gjensidig	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Konvolusjon	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* er konvolusjonsoperatøren
Periodisk funksjon	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$