Funkcja Arccos (x)
Arccos (x), cos -1 (x), odwrotna funkcja cosinus .
Definicja Arccos
Arcus cosinus x jest definiowany jako odwrotna funkcja cosinus x, gdy -1≤x≤1.
Kiedy cosinus y jest równy x:
cos y = x
Wtedy arcus cosinus x jest równy odwrotnej funkcji cosinus x, która jest równa y:
arccos x = cos -1 x = y
(Tutaj cos -1 x oznacza odwrotny cosinus i nie oznacza cosinusa do potęgi -1).
Przykład
arccos 1 = cos -1 1 = 0 rad = 0 °
Wykres arccos
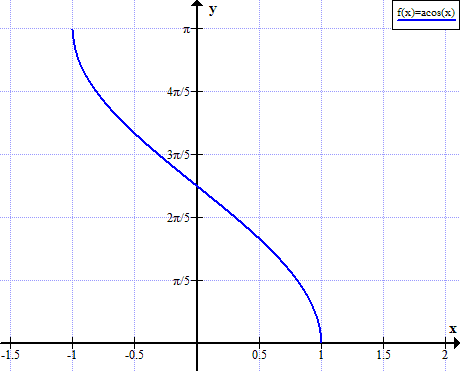
Zasady Arccos
| Nazwa reguły | Reguła |
|---|---|
| Cosinus arccosine | cos (arccos x ) = x |
| Arccosine of cosinus | arccos (cos x ) = x + 2 k π, gdy k ∈ℤ ( k jest liczbą całkowitą) |
| Arccos argumentu negatywnego | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Kąty komplementarne | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Suma Arccos | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Różnica Arccos | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos grzechu x | arccos (sin x ) = - x - (2 k +0,5) π |
| Sinus arccosine |
|
| Styczna arccosine |
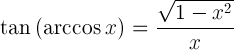 |
| Pochodna arccosine |
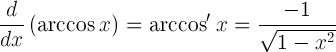 |
| Całka nieoznaczona arccozyny |
|
Stół Arccos
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Zobacz też
- Funkcja cosinus
- Funkcja Arcsine
- Arctanfunction
- Kalkulator Arccos
- Konwerter radianów na stopnie
- Arccos z 0
- Arccos z 1
- Arccos z 2
- Arccos z 3
- Arccos of cos
- Arccos of Sin
- Pochodna Arccos
- Wykres Arccos
- Cos z arccos
- Grzech arccos
- Opalenizna arccos
Advertising