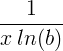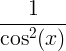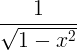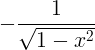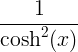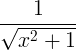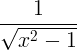Похідні правила

Похідні норми та закони. Таблиця похідних функцій.

Похідне визначення
Похідні правила
Таблиця похідних функцій
Похідні приклади

Похідне визначення

Похідною функції є відношення різниці значення функції f (x) у точках x + Δx та x з Δx, коли Δx нескінченно малий. Похідною є функціональний нахил або нахил дотичної прямої в точці x.

$f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}$

Друга похідна

Друга похідна задається:

Або просто вивести першу похідну:

N-та похідна

П - й похідною розраховується шляхом отримання F (X) п раз.

У п - е похідна дорівнює похідною від (п-1) похідне:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Приклад:

Знайдіть четверту похідну від

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' = = [40 x ³ ] '' = [120 x ² ] '= 240 x

Похідна на графіку функції

Похідною функції є нахил дотичної лінії.

Похідні правила

Правило похідної суми	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Правило похідного продукту	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
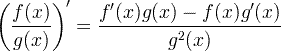Правило похідного коефіцієнта	$\ ліворуч (\ frac {f (x)} {g (x)} \ праворуч) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( х)}$
Правило похідного ланцюга	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Правило похідної суми

Коли a і b - константи.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Приклад:

Знайдіть похідну від:

3 х ² + 4 х.

Відповідно до правила суми:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Правило похідного продукту

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Правило похідного коефіцієнта

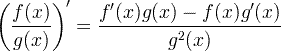
$\ ліворуч (\ frac {f (x)} {g (x)} \ праворуч) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( х)}$

Правило похідного ланцюга

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Це правило можна краще зрозуміти, позначивши Лагранжа:

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

Функція лінійного наближення

Для малого Δx ми можемо отримати наближення до f (x ₀ + Δx), коли ми знаємо f (x ₀ ) та f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Таблиця похідних функцій

Назва функції	Функція	Похідна
Назва функції	f ( x )	f '( x )
Постійний	конст	0
Лінійний	х	1
Потужність	х ^а	сокира ^а-¹
Експоненціальна	e ^x	e ^x
Експоненціальна	a ^x	a ^x ln a
Натуральний логарифм	ln ( x )
Логарифм	log _b ( x )
Синус	гріх х	cos x
Косинус	cos x	-гріх х
Дотична	загар х
Арксин	arcsin x
Арккозін	arccos x
Арктангенс	арктан х
Гіперболічний синус	sinh x	cosh x
Гіперболічний косинус	cosh x	sinh x
Гіперболічний тангенс	tanh x
Зворотний гіперболічний синус	sinh ^-1 x
Обернений гіперболічний косинус	cosh ^-1 x
Зворотний гіперболічний тангенс	танх ^-1 х