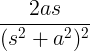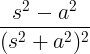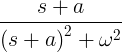Перетворення Лапласа
- Функція перетворення Лапласа
- Таблиця перетворення Лапласа
- Властивості перетворення Лапласа
- Приклади перетворення Лапласа
Перетворення Лапласа перетворює функцію часової області в функцію s-домену шляхом інтеграції від нуля до нескінченності
функції часової області, помножений на e -st .
Перетворення Лапласа використовується для швидкого пошуку рішень для диференціальних рівнянь та інтегралів.
Виведення у часовій області перетворюється на множення на s у s-домені.
Інтеграція у часовій області перетворюється на ділення на s у s-домені.
Функція перетворення Лапласа
Перетворення Лапласа визначається за допомогою оператора L {}:
![]()
Зворотне перетворення Лапласа
Обернене перетворення Лапласа можна обчислити безпосередньо.
Зазвичай зворотне перетворення дається з таблиці перетворень.
Таблиця перетворення Лапласа
| Назва функції | Функція часової області | Перетворення Лапласа |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Постійний | 1 | |
| Лінійний | t | |
| Потужність | т н |
|
| Потужність | t a |
Γ ( a +1) ⋅ s - ( a +1) |
| Експонента | e at |
|
| Синус | гріх на |
|
| Косинус | cos при |
|
| Гіперболічний синус |
sinh at |
|
| Гіперболічний косинус |
кош на |
|
| Вирощування синуса |
т гріх на |
|
| Зростаючий косинус |
t cos при |
|
| Занепадаючий синус |
e -at sin ωt |
|
| Занепадаючий косинус |
e -at cos ωt |
|
| Дельта-функція |
δ ( t ) |
1 |
| Затримана дельта |
δ ( та ) |
e -as |
Властивості перетворення Лапласа
| Назва власності | Функція часової області | Перетворення Лапласа | Прокоментуйте |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Лінійність | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b постійні |
| Зміна масштабу | f ( при ) |
|
a / 0 |
| Shift | e -at f ( t ) | F ( s + a ) | |
| Затримка | f ( ta ) | e - як F ( s ) | |
| Виведення |
|
sF ( s ) - f (0) | |
| N-й вивід |
|
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Потужність | t n f ( t ) |
|
|
| Інтеграція |
|
|
|
| Взаємна |
|
|
|
| Виток | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * - оператор згортки |
| Періодична функція | f ( t ) = f ( t + T ) |
|
Приклади перетворення Лапласа
Приклад №1
Знайдіть перетворення f (t):
f ( t ) = 3 t + 2 t 2
Рішення:
ℒ { t } = 1 / с 2
ℒ { t 2 } = 2 / с 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Приклад №2
Знайдіть обернене перетворення F (s):
F ( s ) = 3 / ( s 2 + s - 6)
Рішення:
Для того, щоб знайти зворотне перетворення, нам потрібно змінити функцію домену s на більш просту форму:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Щоб знайти a і b, ми отримуємо 2 рівняння - один із s-коефіцієнтів, а другий з решти:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Тепер F (s) можна легко перетворити, використовуючи таблицю перетворень для функції експоненти:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Дивіться також
Advertising
КАЛКУЛ
- Обмеження
- Похідна
- Цілісний
- Серія
- Перетворення Лапласа
- Виток
- Символи числення
ШВИДКІ СТОЛИ