لوگرتھم قواعد

کسی نمبر کا بیس بی لوگرتھم اخراج کرنے والا ہوتا ہے جس میں ہمیں نمبر حاصل کرنے کے لئے بیس کو بڑھانا ہوتا ہے ۔

لوگرتھم تعریف

جب b کو y کی طاقت پر اٹھایا جاتا ہے تو x کے برابر ہے۔

b y = x

پھر x کا بیس بی لوگارٹم y کے برابر ہے:

لاگ b ( x ) = y

مثال کے طور پر جب:

2 4 = 16

پھر

لاگ 2 (16) = 4

لوگرتھم معاون فعل کے الٹا فعل کے طور پر

لاگھارتھمک فنکشن ،

y = لاگ b ( x )

مصافاتی فعل کا الٹا فعل ہے ،

x = b y

لہذا اگر ہم x (x/ 0) کے لوگرتھم کے صریحی فعل کا حساب لگائیں ،

f ( f -1 ( x )) = b لاگ b ( x ) = x

یا اگر ہم ایکس کے مفاصلہ فنکشن کے لوگرڈم کا حساب لگاتے ہیں ،

f -1 ( f ( x )) = لاگ b ( b x ) = x

قدرتی لوگارڈم (ایل این)

قدرتی لوگارڈم بیس ای کے لئے ایک لاگاریڈم ہے:

ln ( x ) = لاگ ای ( ایکس )

جب ای مستقل نمبر ہوتا ہے:

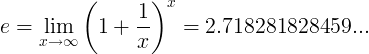
e = \ lim_ {x \ rightarrow \ infty} \ بائیں (1+ \ frac {1} {x} \ دائیں) ^ x = 2.718281828459 ...

یا

e = \ lim_ {x \ رائٹرو 0} \ بائیں (1+ \ دائیں x) ^ rac frac {1} {x}

 

ملاحظہ کریں: قدرتی لوگارڈم

الٹا لوگرتھم حساب

الٹا بیجارتھم (یا اینٹی لوگاریتم) کو بی بی کو لوگرتھم y تک بڑھا کر حساب کیا جاتا ہے:

x = لاگ -1 ( y ) = b y

لوگارتھمک فنکشن

لاگرتھمک فنکشن کی بنیادی شکل یہ ہے:

f ( x ) = لاگ b ( x )

لوگرتھم کے قواعد

اصول نام قاعدہ
لوگرتھم پروڈکٹ رول
 لاگ بی ( x ∙ y ) = لاگ ب ( ایکس ) + لاگ ب ( و )
لوگریتھم قابلیت کا قاعدہ
 لاگ b ( x / y ) = لاگ b ( x ) - لاگ b ( y )
لوگرتھم پاور رول
 لاگ بی ( x y ) = y ∙ لاگ ب ( ایکس )
لوگرتھم بیس سوئچ کا قاعدہ
 لاگ b ( c ) = 1 / لاگ سی ( b )
لوگرتھم بیس چینج رول
 لاگ b ( x ) = لاگ سی ( ایکس ) / لاگ سی ( بی )
لوگرتھم سے ماخوذ
 f ( x ) = لاگ b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
لوگرتھم کا انضمام
 ∫ لاگ b ( x ) dx = x ∙ (لاگ b ( x ) - 1 / ln ( b ) ) + C
منفی نمبر کا لوگرتھم
 جب x ≤ 0 ہوتا ہے تو لاگ b ( x ) کی وضاحت نہیں کی جاتی ہے
0 کا لوگرتھم
 لاگ بی (0) غیر متعینہ ہے
\ lim_ {x \ سے 0 ^ +} \ ٹیکسٹ اپ {لاگ} _ بی (ایکس) = - \ انفٹی
1 کا لوگرتھم
 لاگ بی (1) = 0
اڈے کا لوگرتھم
 لاگ بی ( b ) = 1
لافیتھم آف انفینٹی
 لم لاگ بی ( x ) = ∞ ، جب x → ∞

ملاحظہ کریں: لوگرتھم کے قواعد

 

لوگرتھم پروڈکٹ رول

x اور y کے ضرب کا لوگرتھم x اور y کے لوگرتھم کا جوڑا ہے۔

لاگ بی ( x ∙ y ) = لاگ ب ( ایکس ) + لاگ ب ( و )

مثال کے طور پر:

لاگ 10 (3 ∙ 7) = لاگ 10 (3) + لاگ 10 (7)

لوگریتھم قابلیت کا قاعدہ

x اور y کے تقسیم کا لوگاریتم x اور y کے لوگارتھم کا فرق ہے۔

لاگ b ( x / y ) = لاگ b ( x ) - لاگ b ( y )

مثال کے طور پر:

لاگ ان کریں 10 (3 / 7) = لاگ ان کریں 10 (3) - لاگ ان کریں 10 (7)

لوگرتھم پاور رول

y کی طاقت میں اٹھائے جانے والے x کا لوگرتھم x کے لوگاریتم سے y گنا ہے۔

لاگ بی ( x y ) = y ∙ لاگ ب ( ایکس )

مثال کے طور پر:

لاگ 10 (2 8 ) = 8 ∙ لاگ 10 (2)

لوگرتھم بیس سوئچ کا قاعدہ

c کا بیس بی لوگارٹم b کے بیس سی لوگرتھم سے تقسیم ہوا ہے۔

لاگ b ( c ) = 1 / لاگ سی ( b )

مثال کے طور پر:

لاگ 2 (8) = 1 / لاگ 8 (2)

لوگرتھم بیس چینج رول

x کا بیس بی لوگرتھم x کا بیس سی لوگرتھم ہے جو b کے بیس سی لوگرتھم سے منقسم ہے۔

لاگ b ( x ) = لاگ سی ( ایکس ) / لاگ سی ( بی )

مثال کے طور پر ، کیلکولیٹر میں لاگ 2 (8) کا حساب کرنے کے ل we ، ہمیں بیس کو 10 میں تبدیل کرنے کی ضرورت ہے۔

لاگ 2 (8) = لاگ 10 (8) / لاگ 10 (2)

ملاحظہ کریں: لاگ ان بیس چینج رول

منفی نمبر کا لوگرتھم

جب x <= 0 کی وضاحت نہیں کی جاتی ہے جب x منفی ہے یا صفر کے برابر ہے:

جب x ≤ 0 ہوتا ہے تو لاگ b ( x ) کی وضاحت نہیں کی جاتی ہے

ملاحظہ کریں: منفی نمبر کی لاگ

0 کا لوگرتھم

بیرو بی لاگرتھم صفر کی وضاحت نہیں کی گئی ہے

لاگ بی (0) غیر متعینہ ہے

x کے بیس بی لوگرتھم کی حد ، جب ایکس صفر کے قریب آجاتا ہے تو ، منفی انفینٹی ہے:

\ lim_ {x \ سے 0 ^ +} \ ٹیکسٹ اپ {لاگ} _ بی (ایکس) = - \ انفٹی

ملاحظہ کریں: صفر کا لاگ ان

1 کا لوگرتھم

کسی کا بیس بی لوگرتھم صفر ہے:

لاگ بی (1) = 0

مثال کے طور پر ، ایک میں سے دو بیس لوگارتھم صفر ہے:

لاگ 2 (1) = 0

ملاحظہ کریں: ایک کی لاگ

لافیتھم آف انفینٹی

x کے بیس بی لوگرتھم کی حد ، جب ایکس لامحدود تک پہنچ جاتا ہے ، تو لامحدود ہے:

لم لاگ بی ( x ) = ∞ ، جب x → ∞

ملاحظہ کریں: لافانی کی لاگ ان

اڈے کا لوگرتھم

بی کا بیس بی لوگرتھم ایک ہے:

لاگ بی ( b ) = 1

مثال کے طور پر ، دو کا بیس ٹو لوگرتھم ایک ہے:

لاگ 2 (2) = 1

لوگاریتم مشتق

کب

f ( x ) = لاگ b ( x )

پھر f (ماخوذ) کا مشتق:

f ' ( x ) = 1 / ( x ln ( b ))

دیکھیں: لاگ مشتق

لوگاریتم لازمی

ایکس کے لاگارتھم کا لازمی حصہ:

∫ لاگ b ( x ) dx = x ∙ (لاگ b ( x ) - 1 / ln ( b ) ) + C

مثال کے طور پر:

∫ لاگ 2 ( x ) dx = x ∙ (لاگ 2 ( ایکس ) - 1 / ایل این (2) ) + سی

لوگریتھم قریب

لاگ 2 ( x ) ≈ n + ( ایکس / 2 ن - 1) ،

پیچیدہ لوگرتھم

پیچیدہ نمبر z کے لئے:

z = re iθ = x + iy

پیچیدہ لوگاریتم (n = ...- 2، -1،0،1،2، ...) ہوگا:

لاگ z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · آرکٹان ( y / x ))

لوگرتھم کے مسائل اور جوابات

مسئلہ # 1

کے لئے ایکس تلاش کریں

لاگ 2 ( x ) + لاگ 2 ( x -3) = 2

حل:

پروڈکٹ قاعدہ کا استعمال:

لاگ 2 ( x ∙ ( x -3)) = 2

لاگارتھم کی تعریف کے مطابق لوگیارتھم فارم کو تبدیل کرنا:

x ∙ ( x -3) = 2 2

یا

x 2 -3 x -4 = 0

چوکور مساوات کو حل کرنا:

x 1،2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4، -1

چونکہ منطقی اعداد کے لئے لوگاریتم کی تعریف نہیں کی گئی ہے ، لہذا جواب یہ ہے:

x = 4

مسئلہ # 2

کے لئے ایکس تلاش کریں

لاگ 3 ( x +2) - لاگ 3 ( ایکس ) = 2

حل:

محض قاعدہ کا استعمال:

لاگ 3 (( x +2) / x ) = 2

لاگارتھم کی تعریف کے مطابق لوگیارتھم فارم کو تبدیل کرنا:

( x +2) / x = 3 2

یا

x +2 = 9 x

یا

8 ایکس = 2

یا

x = 0.25

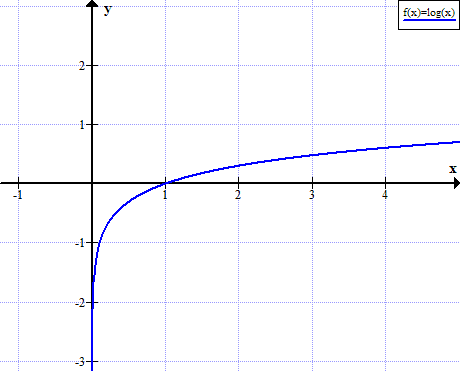
لاگ کا گراف (x)

لاگ (ایکس) ایکس کی حقیقی غیر مثبت اقدار کے لئے بیان نہیں کیا گیا ہے:

لوگارٹم میز

x لاگ ان 10 ایکس لاگ 2 ایکس لاگ ای ایکس
0 غیر متعینہ غیر متعینہ غیر متعینہ
0 + - ∞ - ∞ - ∞
0.0001 -4 -13.287712 -9.210340
0.001 -3 -9.965784 -6.907755
0.01 -2 -6.643856 -4.605170
0.1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

لوگرتھم کیلکولیٹر ►

 

بھی دیکھو

Advertising

الجبرا
ریپڈ ٹیبلیاں