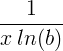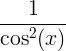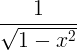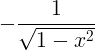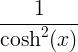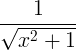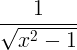Quy tắc phái sinh
Các quy tắc và luật phái sinh. Đạo hàm của bảng hàm.
Định nghĩa phái sinh
Đạo hàm của một hàm là tỷ số giữa hiệu của giá trị hàm f (x) tại các điểm x + Δx và x với Δx, khi Δx nhỏ vô cùng. Đạo hàm là hệ số góc của hàm số hoặc hệ số góc của đường tiếp tuyến tại điểm x.
![]()
Dẫn xuất thứ hai
Đạo hàm thứ hai được cho bởi:
![]()
Hoặc đơn giản là lấy đạo hàm đầu tiên:
![]()
Đạo hàm thứ n
Đạo hàm thứ n được tính bằng cách lấy f (x) n lần.
Đạo hàm thứ n bằng đạo hàm của đạo hàm (n-1):
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Thí dụ:
Tìm đạo hàm thứ tư của
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Đạo hàm trên đồ thị của hàm số
Đạo hàm của một hàm là độ dốc của đường tiếp tuyến.
Quy tắc phái sinh
| Quy tắc tổng phái sinh |
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Quy tắc sản phẩm phái sinh |
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Quy tắc thương số phái sinh |
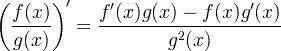 |
| Quy tắc chuỗi phái sinh |
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Quy tắc tổng phái sinh
Khi a và b là hằng số.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Thí dụ:
Tìm đạo hàm của:
3 x 2 + 4 x.
Theo quy tắc tổng:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Quy tắc sản phẩm phái sinh
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Quy tắc thương số phái sinh
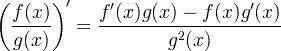
Quy tắc chuỗi phái sinh
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Quy tắc này có thể được hiểu rõ hơn với ký hiệu Lagrange:
![]()
Hàm gần đúng tuyến tính
Đối với Δx nhỏ, chúng ta có thể nhận được một giá trị gần đúng với f (x 0 + Δx), khi chúng ta biết f (x 0 ) và f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Đạo hàm của bảng hàm
| Tên chức năng | Chức năng | Phát sinh |
|---|---|---|
|
f ( x ) |
f '( x ) | |
| Không thay đổi |
hăng sô |
0 |
| Tuyến tính |
x |
1 |
| Quyền lực |
x a |
rìu a- 1 |
| số mũ |
e x |
e x |
| số mũ |
một x |
a x ln a |
| Lôgarit tự nhiên |
ln ( x ) |
|
| Lôgarit |
log b ( x ) |
|
| Sin |
tội lỗi x |
cos x |
| Cô sin |
cos x |
-sin x |
| Tiếp tuyến |
tan x |
|
| Arcsine |
arcsin x |
|
| Arccosine |
arccos x |
|
| Arctangent |
arctan x |
|
| Sin hyperbol |
sinh x |
cosh x |
| Cosin hyperbolic |
cosh x |
sinh x |
| Tiếp tuyến hyperbol |
tanh x |
|
| Sin hyperbol nghịch đảo |
sinh -1 x |
|
| Cosin hyperbol nghịch đảo |
cosh -1 x |
|
| Tiếp tuyến hyperbol nghịch đảo |
tanh -1 x |
|
Ví dụ phái sinh
Ví dụ 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Ví dụ số 2
f ( x ) = sin (3 x 2 )
Khi áp dụng quy tắc chuỗi:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Kiểm tra đạo hàm thứ hai
Khi đạo hàm cấp một của hàm số bằng 0 tại điểm x 0 .
f '( x 0 ) = 0
Khi đó đạo hàm cấp hai tại điểm x 0 , f '' (x 0 ), có thể chỉ ra loại điểm đó:
|
f '' ( x 0 )/ 0 |
địa phương tối thiểu |
|
f '' ( x 0 ) <0 |
tối đa địa phương |
|
f '' ( x 0 ) = 0 |
không xác định |
Xem thêm
Advertising
TÍNH TOÁN
- Giới hạn
- Phát sinh
- Tích phân
- Loạt
- Biến đổi laplace
- Convolution
- Ký hiệu giải tích
BẢNG RAPID