Разпределение на вероятностите

В вероятност и статистика разпределението е характеристика на случайна променлива, описва вероятността на случайната променлива във всяка стойност.

Всяко разпределение има определена функция на плътност на вероятността и функция на разпределение на вероятностите.

Въпреки че има неопределен брой вероятностни разпределения, има няколко често използвани разпределения.

Кумулативна функция на разпределение

Разпределението на вероятностите се описва чрез кумулативната функция на разпределение F (x),

което е вероятността случайна променлива X да получи стойност по-малка или равна на x:

F ( x ) = P ( X ≤ x )

Непрекъснато разпространение

Кумулативната функция на разпределение F (x) се изчислява чрез интегриране на функцията на вероятностна плътност f (u) на непрекъсната случайна променлива X.

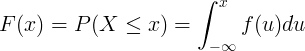
Дискретно разпределение

Кумулативната функция на разпределение F (x) се изчислява чрез сумиране на вероятностната масова функция P (u) на дискретна случайна променлива X.

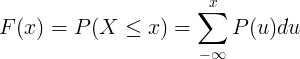
Таблица за непрекъснати разпределения

Непрекъснатото разпределение е разпределението на непрекъсната случайна величина.

Пример за непрекъснато разпространение

...

Таблица за непрекъснати разпределения

Име на разпространението Символ за разпределение Функция на плътността на вероятността (pdf) Означава Дисперсия
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Нормално / гаус

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Униформен

X ~ U ( a , b )

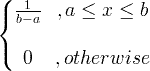 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, в противен случай \ end {матрица} \ frac {(ba) ^ 2} {12}
Експоненциално X ~ опит (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
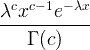Гама X ~ гама ( c , λ) \ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Чи квадрат

X ~ χ 2 ( k )

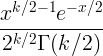 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Гама (k / 2)}

k

2 к
Уишарт        
F

X ~ F ( k 1 , k 2 )

      
Бета        
Weibull        
Дневник-нормален

X ~ LN (μ, σ 2 )

      
Рейли        
Коши        
Дирихле        
Лаплас        
Леви        
Ориз        
Студентски t        

Таблица за дискретни разпределения

Дискретно разпределение е разпределението на дискретна случайна величина.

Пример за дискретно разпределение

...

Таблица за дискретни разпределения

Име на разпространението Символ за разпределение Вероятностна функция на масата (pmf) Означава Дисперсия
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Двучленен

X ~ Кошче ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Поасон

X ~ Поасон (λ)

λ ≥ 0

λ

λ

Униформен

X ~ U ( a, b )

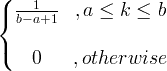 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, в противен случай \ end {матрица} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Геометрични

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Хипергеометрични

X ~ HG ( N , K , n )

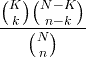N = 0,1,2, ...

К = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Бернули

X ~ Берн ( p )

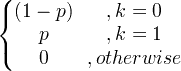 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, в противен случай \ end {матрица}

p

p (1- p )

 

Вижте също

Advertising

ВЕРОЯТНОСТ И СТАТИСТИКА
БЪРЗИ МАСИ