Стандартно отклонение

При вероятност и статистика стандартното отклонение на случайна променлива е средното разстояние на случайна променлива от средната стойност.

Той представя как случайната променлива се разпределя близо до средната стойност. Малко стандартно отклонение показва, че случайната променлива се разпределя близо до средната стойност. Голямото стандартно отклонение показва, че случайната променлива се разпределя далеч от средната стойност.

Формула за дефиниция на стандартно отклонение

Стандартното отклонение е квадратният корен от дисперсията на случайна променлива X, със средна стойност от μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

От дефиницията на стандартното отклонение можем да получим

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Стандартно отклонение на непрекъсната случайна променлива

За непрекъсната случайна променлива със средна стойност μ и функция на плътността на вероятността f (x):

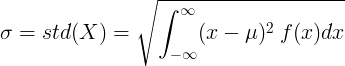
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

или

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Стандартно отклонение на дискретна случайна величина

За дискретна случайна променлива X със средна стойност μ и функция на вероятността маса P (x):

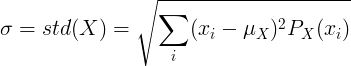
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

или

\ sigma = std (X) = \ sqrt {\ ляво [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ дясно] - \ mu ^ 2}

 

Разпределение на вероятностите ►

 

Вижте също

Advertising

ВЕРОЯТНОСТ И СТАТИСТИКА
БЪРЗИ МАСИ