Cothromóid Chearnach
Is é atá sa chothromóid chearnach ná polaiméanóm dara hord le 3 chomhéifeacht - a , b , c .
Tugtar an chothromóid chearnach trí:
tua 2 + bx + c = 0
Tugtar an tuaslagán don chothromóid chearnach le 2 uimhir x 1 agus x 2 .
Is féidir linn an chothromóid chearnach a athrú go foirm:
( x - x 1 ) ( x - x 2 ) = 0
Foirmle Cearnach
Tugtar an réiteach ar an gcothromóid chearnach leis an bhfoirmle chearnach:
![]()
Tugtar idirdhealaitheach ar an slonn taobh istigh den fhréamh cearnach agus tugtar Δ:
Δ = b 2 - 4 ac
An fhoirmle chearnach le nodaireacht idirdhealaitheach:
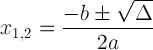
Tá an abairt seo tábhachtach mar is féidir léi insint dúinn faoin réiteach:
- Nuair a bhíonn Δ/ 0 ann, tá 2 fhíorfhréamh x 1 = (- b + √ Δ ) / (2a) agus x 2 = (- b-√ Δ ) / (2a) .
- Nuair a bhíonn Δ = 0, tá fréamh amháin x 1 = x 2 = -b / (2a) .
- Nuair a bhíonn Δ <0, níl fíorfhréamhacha ann, tá 2 fhréamh casta ann:
x 1 = (- b + i√ -Δ ) / (2a) agus x 2 = (- bi√ -Δ ) / (2a) .
Fadhb # 1
3 x 2 +5 x +2 = 0
réiteach:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Fadhb # 2
3 x 2 -6 x +3 = 0
réiteach:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Fadhb # 3
x 2 +2 x +5 = 0
réiteach:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Níl aon réitigh dáiríre ann. Is uimhreacha casta iad na luachanna:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Graf Feidhm Chearnach
Is í an fheidhm chearnach feidhm pholaimialtach dara hord:
f ( x ) = tua 2 + bx + c
Is iad na réitigh ar an gcothromóid chearnach fréamhacha na feidhme cearnacha, is iad sin pointí trasnaithe an ghraif chearnach feidhme leis an x-ais, nuair a
f ( x ) = 0
Nuair a bhíonn 2 phointe trasnaithe den ghraf leis an x-ais, tá 2 thuaslagán sa chothromóid chearnach.
Nuair a bhíonn 1 phointe trasnaithe den ghraf leis an x-ais, tá 1 tuaslagán sa chothromóid chearnach.
Nuair nach bhfuil aon phointe trasnaithe den ghraf leis an x-ais, ní fhaighimid fíor-réitigh (nó 2 réiteach casta).
Féach freisin
Advertising