Logarithm Nádúrtha - ln (x)

Is é logarithm nádúrtha an logarithm go bun e uimhir.

Sainmhíniú ar logarithm nádúrtha

Cathain

e y = x

Ansin bun e logarithm de x is

ln ( x ) = log e ( x ) = y

 

Is í an e tairiseach nó uimhir Euler:

e ≈ 2.71828183

Ln mar fheidhm inbhéartach na feidhme easpónantúla

Is í an fheidhm logartamach nádúrtha ln (x) feidhm inbhéartach na feidhme easpónantúla e x .

Le haghaidh x/ 0,

f ( f -1 ( x )) = e ln ( x ) = x

Nó

f -1 ( f ( x )) = ln ( e x ) = x

Rialacha agus airíonna logarithm nádúrtha

Ainm na rialach Riail Sampla
Riail táirge

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
Riail go leor

ln ( x / y ) = ln ( x ) - ln ( y )

ln (3 / 7) = ln (3) - ln (7)
Riail chumhachta

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
díorthach ln
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
ln lárnach
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C.  
ln d’uimhir dhiúltach
 Tá ln ( x ) neamhshainithe nuair a bhíonn x ≤ 0  
ln de nialas
 Tá ln (0) neamhshainithe  
 
ln de cheann
 ln (1) = 0  
ln an éigríochta
 lim ln ( x ) = ∞, nuair a bhíonn x → ∞  
Céannacht Euler ln (-1) = i π  

 

Riail táirge logarithm

Is é logarithm iolrú x agus y suim logarithm x agus logarithm y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Mar shampla:

log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)

Riail chomhrann logarithm

Is é logarithm roinn x agus y an difríocht idir logarithm x agus logarithm y.

log b ( x / y ) = log b ( x ) - log b ( y )

Mar shampla:

logáil 10 (3 / 7) = logáil 10 (3) - logáil 10 (7)

Riail cumhachta logarithm

Is é logarithm x a ardaíodh do chumhacht y ná y logarithm x.

log b ( x y ) = y ∙ log b ( x )

Mar shampla:

log 10 (2 8 ) = 8 ∙ log 10 (2)

Díorthach logarithm nádúrtha

Is é díorthach na feidhme logarithm nádúrtha an fheidhm chómhalartach.

Cathain

f ( x ) = ln ( x )

Is é díorthach f (x):

f ' ( x ) = 1 / x

Comhtháite de logarithm nádúrtha

Tugtar an chuid dhílis den fheidhm logartamach nádúrtha trí:

Cathain

f ( x ) = ln ( x )

Is é gné dhílis f (x):

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

Ln de 0

Tá logarithm nádúrtha nialas neamhshainithe:

Tá ln (0) neamhshainithe

Is í an teorainn gar do 0 de logarithm nádúrtha x, nuair a bhíonn x ag druidim le nialas, lúide an Infinity:

Ln de 1

Is é ná logarithm nádúrtha ceann amháin ná nialas:

ln (1) = 0

Ln an éigríochta

Tá teorainn logarithm nádúrtha an éigríochta, nuair a bhíonn x ag druidim leis an éigríocht cothrom leis an infinacht:

lim ln ( x ) = ∞, nuair a bhíonn x → ∞

Logarithm casta

Maidir le huimhir chasta z:

z = re iθ = x + iy

Is é an logarithm casta (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

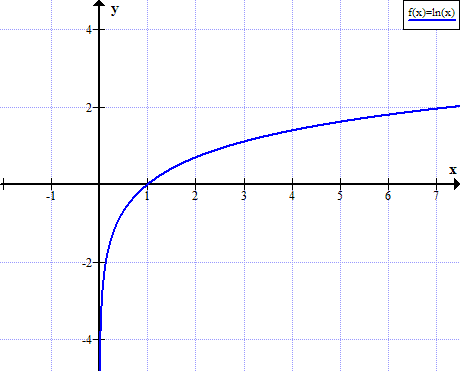
Graf de ln (x)

Ní shainmhínítear ln (x) le haghaidh fíorluachanna neamh-dhearfacha x:

Tábla logarithim nádúrtha

x ln x
0 neamhshainithe
0 + - ∞
0.0001 -9.210340
0.001 -6.907755
0.01 -4.605170
0.1 -2.302585
1 0
2 0.693147
e ≈ 2.7183 1
3 1.098612
4 1.386294
5 1.609438
6 1.791759
7 1.945910
8 2.079442
9 2.197225
10 2.302585
20 2.995732
30 3.401197
40 3.688879
50 3.912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4.605170
200 5.298317
300 5.703782
400 5.991465
500 6.214608
600 6.396930
700 6.551080
800 6.684612
900 6.802395
1000 6.907755
10000 9.210340

 

Rialacha logarithm ►

 

Féach freisin

Advertising

ALGEBRA
TÁBLAÍ RAPID